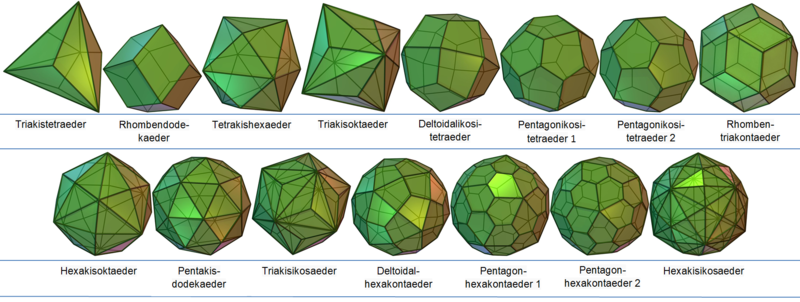
Catalanische Körper: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Pentagonhexakontaeder) |
(→Pentagonikositetraeder) |
||
| Zeile 194: | Zeile 194: | ||
<center> | <center> | ||
<popup name=""> | <popup name=""> | ||
| − | [[File: | + | [[File:Pentagonalicositetrahedronccw.jpg|x200px]] <font size="7"> « </font> <font size="6">=</font> <font size="7"> » </font> [[|x200px]] |
</popup> | </popup> | ||
</center> | </center> | ||
| Zeile 205: | Zeile 205: | ||
<center> | <center> | ||
<popup name=""> | <popup name=""> | ||
| − | [[File: | + | [[File:Pentagonalicositetrahedroncw.jpg|x200px]] <font size="7"> « </font> <font size="6">=</font> <font size="7"> » </font> [[|x200px]] |
</popup> | </popup> | ||
</center> | </center> | ||
Version vom 11. November 2013, 23:45 Uhr
|
|
Allgemeines
Triakistetraeder
Rhombendodekaeder
Triakisoktaeder
Tetrakishexaeder
Deltoidalikositetraeder
Großes Rhombenkuboktaeder
Rhombentriakontaeder
Triakisikosaeder
Pentakisdodekaeder
Pentagonikositetraeder
Deltoidalhexakontaeder
Großes Rhombenikosidodekaeder
Pentagonhexakontaeder
|