Catalanische Körper: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Allgemeines)
Zeile 52: Zeile 52:
  
 
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
 
{|style="background:#F0E9CA" border="0" cellspacing="0" cellpadding="4"
−
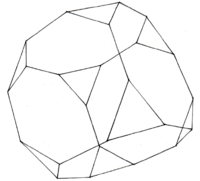
Bei Catalanischen Körpern wird die "Oberfläche aus kongruenten ungleichseitigen [...] Vielecken einer einzigen Flächenart gebildet"<ref name="">Paul Adam, Arnold Wyss, Platonische und Archimedische Körper; ihre Sternformen und polaren Gebilde, Stuttgart 1994, S.77</ref>, die "Ecken [werden] von ungleich vielen Kanten gebildet"<ref>Ebd., a. a. O.</ref> werden und die "Kanten ungleich lang" <ref>Ebd., a. a. O.</ref> sind.
+
Bei Catalanischen Körpern wird die "Oberfläche aus kongruenten ungleichseitigen [...] Vielecken einer einzigen Flächenart gebildet"<ref name="">Paul Adam, Arnold Wyss, Platonische und Archimedische Körper; ihre Sternformen und polaren Gebilde, Stuttgart 1994, S.77</ref>, die "Ecken [werden] von ungleich vielen Kanten gebildet"<ref>Ebd., a. a. O.</ref> und die "Kanten [sind] ungleich lang" <ref>Ebd., a. a. O.</ref>.  
  
  

Version vom 11. November 2013, 23:55 Uhr

Platonische Körper Briefpapier Button.pngPlatonische Körper
Archimedische Körper Briefpapier Button.pngArchimedische Körper
Catalanische Körper.jpgCatalanische Körper
Sternkörper Briefpapier Button.pngSternkörper





C A T A L A N I S C H E   K Ö R P E R                            



Die Catalanischen Körper werden auch dualarchimedische Körper genannt, da jeder Catalanische einen Archimedischen Körper besitzt, zu welchem er dual ist.

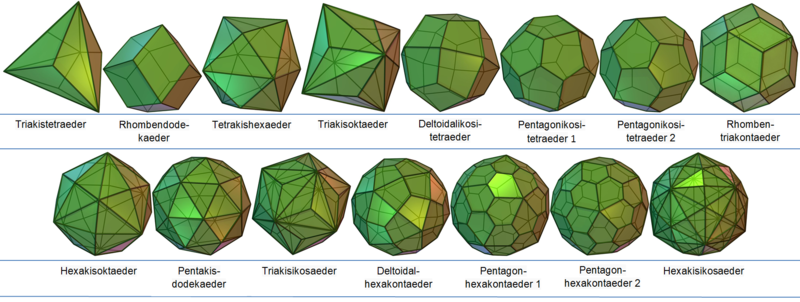
Zusammenfassung aller Catalanischen Körper.png

Inhaltsverzeichnis

 [Verbergen] 

Allgemeines

Bei Catalanischen Körpern wird die "Oberfläche aus kongruenten ungleichseitigen [...] Vielecken einer einzigen Flächenart gebildet"[1], die "Ecken [werden] von ungleich vielen Kanten gebildet"[2] und die "Kanten [sind] ungleich lang" [3].

Triakistetraeder


Rhombendodekaeder


Triakisoktaeder

Hexaederstumpf.png

Der Hexaederstumpf besitzt: 

         10 Ecken
         10 Ecken
         10 Ecken

Er kann durch das Abschneiden von Ecken aus dem Hexaeder gebildet werden


Tetrakishexaeder

Deltoidalikositetraeder


Großes Rhombenkuboktaeder


Rhombentriakontaeder


Triakisikosaeder

Pentakisdodekaeder


Pentagonikositetraeder

Deltoidalhexakontaeder

Großes Rhombenikosidodekaeder


Pentagonhexakontaeder




Trunc-icosa.jpg[4]

  • ↑ Paul Adam, Arnold Wyss, Platonische und Archimedische Körper; ihre Sternformen und polaren Gebilde, Stuttgart 1994, S.77
  • ↑ Ebd., a. a. O.
  • ↑ Ebd., a. a. O.
  • ↑ Ikosaederstumpf

    • Von „http://rmg.zum.de/index.php?title=Benutzer:Thamm_Pascal/Platonische_Körper/Weiterführende_Inhalte/Catalanische_Körper&oldid=54797“

    Navigationsmenü