Beweis 2: Unterschied zwischen den Versionen

Version vom 23. Dezember 2010, 03:28 Uhr

Zu zeigen: 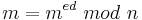$\quad m= m^{ed}\ mod\ n$
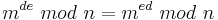
$\quad m^{de}\ mod\ n = m^{ed}\ mod\ n$

Der Beweis basiert auf dem Satz von Euler und dem Satz von Fermat.

Danach gilt: 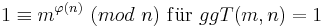$1\equiv m^{\varphi(n)}\ (mod\ n)\ \mathrm{f{\ddot u}r}\ ggT(m,n)=1$
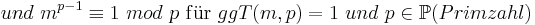
$und\ m^{p-1}\equiv 1\ mod\ p\ \mathrm{f{\ddot u}r}\ ggT(m,p) = 1\ und\ p \in \mathbb P (Primzahl)$

1. Mit 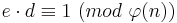$e\cdot d\equiv 1\ (mod\ \varphi(n))$ , d.h. 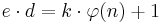$e\cdot d = k\cdot \varphi(n)+1$ gilt:
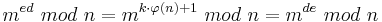$m^{ed}\ mod\ n = m^{k\cdot \varphi(n)+1}\ mod\ n = m^{de}\ mod\ n$ .

2. Es bleibt also zu zeigen: 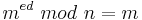$m^{ed}\ mod\ n = m$
Man unterscheidet nun die Fälle, dass p m teilt, und das p m nicht teilt. Falls p Teiler von m ist, gilt (mit einem passenden 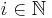$i \in \N$ )

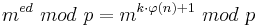
$m^{ed}\ mod\ p = m^{k\cdot \varphi(n)+1}\ mod\ p$
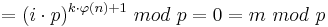
$\quad = (i\cdot p)^{k\cdot \varphi(n)+1}\ mod\ p = 0 = m\ mod\ p$
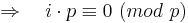
$\Rightarrow \quad i\cdot p \equiv 0\ (mod\ p)$

Ist p nicht Teiler von m, dann gilt: ggT (p,m) = 1, da p eine Primzahl ist.

Die Sätze von Euler und Fermat sind anwendbar und es gilt:

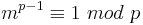
$m^{p-1} \equiv 1\ mod\ p$

Da 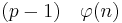$(p-1)\quad \varphi(n)$ teilt, gilt weiterhin:

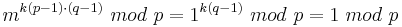
$m^{k(p-1)\cdot (q-1)}\ mod\ p = 1^{k(q-1)}\ mod\ p =1\ mod\ p$

Also auch 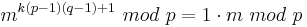$m^{k(p-1)(q-1)+1}\ mod\ p = 1\cdot m\ mod\ p$

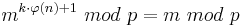
Und damit: $m^{k\cdot \varphi(n)+1}\ mod\ p = m\ mod\ p$

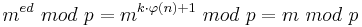
Also: $m^{ed}\ mod\ p = m^{k\cdot \varphi(n)+1}\ mod\ p = m\ mod\ p$

Analog gilt für 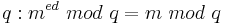$q: m^{ed}\ mod\ q = m\ mod\ q$
Es existiert weiterhin 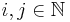$i,j \in \N$ mit

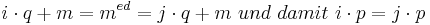
$i\cdot q +m = m^{ed} = j\cdot q +m\ und\ damit\ i\cdot p = j\cdot p$

da p und q Primzahlen sind, gilt es gibt 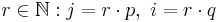$\ r \in \N : j = r\cdot p,\ i = r\cdot q$

Damit gilt: 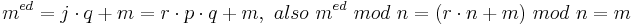$m^{ed} = j\cdot q+m = r\cdot p\cdot q +m,\ also\ m^{ed}\ mod\ n = (r\cdot n + m)\ mod\ n = m$

Damit ist eindeutig gezeigt, dass sich die Nachricht m aus c wieder gewinnen lässt. □

zurück zum RSA-Algorithmus

zurück zur Übersicht

Der auf dieser Seite dargestellte Beweis stammt aus [5, S.324 f.]
siehe dazu Literaturverzeichnis

@@ Zeile 5: / Zeile 5: @@
 <br>
 Danach gilt: <math>1\equiv m^{\varphi(n)}\ (mod\ n)\ \mathrm{f{\ddot u}r}\ ggT(m,n)=1</math><br>
-<math>und\ m^{p-1}\equiv 1\ (mod\ p)\ \mathrm{f{\ddot u}r}\ ggT(m,p) = 1\ und\ p \in \mathbb P (Primzahl)</math><br>
+<math>und\ m^{p-1}\equiv 1\ mod\ p\ \mathrm{f{\ddot u}r}\ ggT(m,p) = 1\ und\ p \in \mathbb P (Primzahl)</math><br>
 <br>
 . Mit <math>e\cdot d\equiv 1\ (mod\ \varphi(n))</math>, d.h. <math>e\cdot d = k\cdot \varphi(n)+1</math> gilt:<br>
-<math>m^{ed}\ (mod\ n) = m^{k\cdot \varphi(n)+1}\ (mod\ n) = m^{de}\ (mod\ n)</math>.<br>
+<math>m^{ed}\ mod\ n = m^{k\cdot \varphi(n)+1}\ mod\ n = m^{de}\ mod\ n</math>.<br>
 <br>
-. Es bleibt also zu zeigen:  <math>m^{ed}\ (mod\ n) = m</math><br>
+. Es bleibt also zu zeigen:  <math>m^{ed}\ mod\ n = m</math><br>
 Man unterscheidet nun die Fälle, dass p m teilt, und das p m nicht teilt. Falls p Teiler von m ist, gilt (mit einem passenden <math>i \in \N</math>)<br><br>
-<math>m^{ed}\ (mod\ p) = m^{k\cdot \varphi(n)+1}\ (mod\ p)</math><br>
+<math>m^{ed}\ mod\ p = m^{k\cdot \varphi(n)+1}\ mod\ p</math><br>
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math>\quad  = (i\cdot p)^{k\cdot \varphi(n)+1}\ (mod\ p) = 0 = m\ (mod\ p)</math><br>
+&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math>\quad  = (i\cdot p)^{k\cdot \varphi(n)+1}\ mod\ p = 0 = m\ mod\ p</math><br>
 <math>\Rightarrow \quad i\cdot p \equiv 0\ (mod\ p)</math><br>
 <br>
@@ Zeile 20: / Zeile 20: @@
 Die Sätze von Euler und Fermat sind anwendbar und es gilt:<br>
 <br>
-<math>m^{p-1} \equiv 1\ (mod\ p)</math><br>
+<math>m^{p-1} \equiv 1\ mod\ p</math><br>
 <br>
 Da <math>(p-1)\quad \varphi(n)</math> teilt, gilt weiterhin:<br>
 <br>
-<math>m^{k(p-1)\cdot (q-1)}\ (mod\ p) = 1^{k(q-1)}\ (mod\ p) =1\  (mod\ p)</math><br>
+<math>m^{k(p-1)\cdot (q-1)}\ mod\ p = 1^{k(q-1)}\ mod\ p =1\  mod\ p</math><br>
 <br>
-Also auch <math>m^{k(p-1)(q-1)+1}\ (mod\ p) = 1\cdot m\ (mod\ p)</math><br>
+Also auch <math>m^{k(p-1)(q-1)+1}\ mod\ p = 1\cdot m\ mod\ p</math><br>
 <br>
-Und damit: <math>m^{k\cdot \varphi(n)+1}\ (mod\ p) = m\ (mod\ p)</math><br>
+Und damit: <math>m^{k\cdot \varphi(n)+1}\ mod\ p = m\ mod\ p</math><br>
 <br>
-Also: <math>m^{ed}\ (mod\ p) = m^{k\cdot \varphi(n)+1}\ mod\ p = m\ (mod\ p)</math><br>
+Also: <math>m^{ed}\ mod\ p = m^{k\cdot \varphi(n)+1}\ mod\ p = m\ mod\ p</math><br>
 <br>
-Analog gilt für <math>q: m^{ed}\ (mod\ q) = m\ (mod\ q)</math><br>
+Analog gilt für <math>q: m^{ed}\ mod\ q = m\ mod\ q</math><br>
 Es existiert weiterhin <math>i,j \in \N</math> mit<br>
 <br>
@@ Zeile 39: / Zeile 39: @@
 da p und q Primzahlen sind, gilt es gibt <math>\ r \in \N : j = r\cdot p,\ i = r\cdot q</math><br>
 <br>
-Damit gilt: <math>m^{ed} = j\cdot q+m = r\cdot p\cdot q +m,\ also\ m^{ed}\ (mod\ n) = (r\cdot n + m)\ (mod\ n) = m</math><br>
+Damit gilt: <math>m^{ed} = j\cdot q+m = r\cdot p\cdot q +m,\ also\ m^{ed}\ mod\ n = (r\cdot n + m)\ mod\ n = m</math><br>
 <br>
 Damit ist eindeutig gezeigt, dass sich die Nachricht m aus c wieder gewinnen lässt. □<br>

Beweis 2: Unterschied zwischen den Versionen

Version vom 23. Dezember 2010, 03:28 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Hilfen

Oberstufe

Studien- und Berufsorientierung am RMG

Werkzeuge