Grieninger Sebastian/Facharbeit1/reine Stimmung: Unterschied zwischen den Versionen
(→Der Aufbau der reinen Stimmung) |
(→Der Aufbau der reinen Stimmung) |
||
| Zeile 81: | Zeile 81: | ||
Die Gleichung: <math> \frac {81}{80} = 2^x \cdot \frac {3}{2}^y \cdot \frac {5}{4}^z \ fuer \ x , y , z \in \Z </math> hat die eindeutige Lösung, als "Tripellogarithmus" bezeichnet: x = -2, y = 4 und z = -1. <br><br> | Die Gleichung: <math> \frac {81}{80} = 2^x \cdot \frac {3}{2}^y \cdot \frac {5}{4}^z \ fuer \ x , y , z \in \Z </math> hat die eindeutige Lösung, als "Tripellogarithmus" bezeichnet: x = -2, y = 4 und z = -1. <br><br> | ||
Damit gilt für das Intervall i mit dem Frequenzverhältnis <math>\textstyle \frac {81}{80}</math> die Beziehung <math>i = - 2 \cdot Ok + 4 \cdot Q - T</math>. (Siehe synthonisches Komma).<br><br> | Damit gilt für das Intervall i mit dem Frequenzverhältnis <math>\textstyle \frac {81}{80}</math> die Beziehung <math>i = - 2 \cdot Ok + 4 \cdot Q - T</math>. (Siehe synthonisches Komma).<br><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Eine bekannte Orgel, die in reiner Stimmung gestimmt ist, ist die Praetoriusorgel der Universität Freiburg. Um einen Einblick in die Klangwelt der reinen Stimmung zu bekommen findet sich [http://podcast2.ruf.uni-freiburg.de/ub/casts/audio-cd/sachs_schroeder_musik_praetoriusorgel/01.mp3 hier] eine Aufnahme von dieser Orgel. (Wer noch mehr Aufnahmen wünscht, wird [http://podcasts.uni-freiburg.de/podcast_content?id_content=64 hier] fündig) | Eine bekannte Orgel, die in reiner Stimmung gestimmt ist, ist die Praetoriusorgel der Universität Freiburg. Um einen Einblick in die Klangwelt der reinen Stimmung zu bekommen findet sich [http://podcast2.ruf.uni-freiburg.de/ub/casts/audio-cd/sachs_schroeder_musik_praetoriusorgel/01.mp3 hier] eine Aufnahme von dieser Orgel. (Wer noch mehr Aufnahmen wünscht, wird [http://podcasts.uni-freiburg.de/podcast_content?id_content=64 hier] fündig) | ||
Version vom 23. Dezember 2010, 02:12 Uhr
Der Aufbau der reinen Stimmung
Da die pythagoreische Stimmung, wie oben beschrieben, v.a. in der Mehrstimmigkeit Probleme hatte, musste ein anderes System entwickelt werden.
Man setzt nun neben Quinte und Oktave auch die (große) Terz fest, statt sie aus den gestapelten Quinten, wie die Pythagoreer zu berechnen, teilte man eine Saite in 5 Teile und erhielt das Verhältnis 5:4 und berechnete ausgehend von den 3 Basisintervallen die restlichen Intervalle. Die reine Stimmung wird auch als diatonische und als natürliche Stimmung bezeichnet.
Für Interessierte: Berechnung der Intervalle durch Vektorrechnung
Am Beispiel der Tonart C-Dur werde ich den Aufbau der natürlichen Skala beschreiben.
Wir starten beim Ton C und gehen nun eine reine Quinte aufwärts.
Die reine Quinte hat das bekannte Verhältnis 3:2. Da sich Quinte und Quarte zu einer Oktave ergänzen, folgt analog für die Quarte das Verhältnis 4:3 und für die Oktave 2:1.
Wenn wir die größtmögliche Zahl konsonanter Intervalle erhalten wollen, stehen uns für das nächste Intervall 2 Schritte zur Verfügung: die große Terz mit dem Verhältnis 5:4 oder die kleine Terz mit dem Verhältnis 6:5. „Wir wählen den ersten, weil dieser eine größere Anzahl von Konsonanzen höheren „Grades“ garantiert.“[1]
„Je niedriger die im Frequenzverhältnis vorkommenden Zahlen, umso höher ist die subjektiv empfundene Konsonanz“[2]
| Intervall | Frequenzverhältnis | größte vorkommende Zahl |
|---|---|---|
| Prime | 1 : 1 | 1 |
| Oktave | 2 : 1 | 2 |
| Quinte | 3 : 2 | 3 |
| Quarte | 4 : 3 | 4 |
| Große Terz | 5 : 4 | 5 |
| Kleine Terz | 6 : 5 | 6 |
Die Terz mit dem Verhältnis 5:4 entspricht der großen Terz, also der Durterz. Das Verhältnis 6:5 entspricht der kleinen Terz, der Mollterz.
In der natürlichen Stimmung ergänzen sich große und kleine Terz zu einer Quinte.
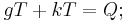
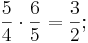
Den großen Ganzton erhält man, wenn man 2 Quinten nach oben geht und eine Oktave nach unten (vgl. pythagoreische Stimmung)
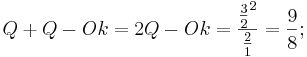
Der kleine Ganzton ergibt sich, wenn man von der großen Terz einen Ganzton abzieht, oder eine Oktave und große Terz nach oben geht und dann 2 Quinten nach unten geht.
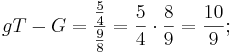
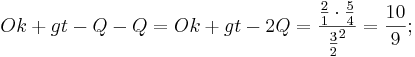
Die (große) Sexte erreicht man, wenn man eine Oktave und eine große Terz nach oben geht und anschließend eine Quinte nach unten:
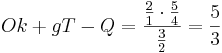
Die 7. Stufe der Dur-Tonleiter, die kleine Septime, ergibt sich, wenn man auf die Quinte eine große Terz setzt.
Q + gT = große Septime =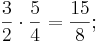 
Damit ergibt sich für die C-Dur Tonleiter folgendes Bild:
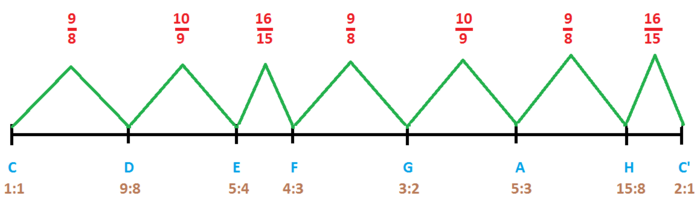
Damit ergibt sich die fortlaufende Proportion (in Hertz):
| c | d | e | f | g | a | h | c' |
| 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 |
die wie folgt entsteht:
Für c wird die Frequenz 24 Hertz (H(c) = 24 Hertz) festgelegt. Von hier rechnet man die Frequenzen der Tonleiter aus. Also für die Quinte g gilt:
.
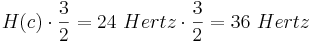Analog dazu werden die anderen Schritte berechnet.
Eine fortlaufende Proportion wird immer durch die kleinst möglichten, ganzzahligen Verhältnisse der Frequenzen gebildet. (In diesem Fall aufbauend auf 24 Hertz).
Nun müsste die Quinte von der 2. auf die 6. Stufe (d-a), die durch die Verhältniszahlen 27 und 40 ausgedrückt wird, dem Quintverhältnis 2:3 entsprechen. Wenn man es jedoch durch eine Rechnung nachprüfen will, ergibt sich folgendes:
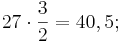
d.h. die Quinte zwischen d und a ist zu klein. Das Verhältnis beträgt: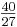 
= 
;
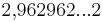„Das Verhältnis der reinen Quinte zur „kurzen“ Quinte lautet also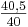 
oder (erweitert) 
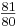“[3]
Diese Abweichung wird das syntonische Komma genannt.
Die Gleichung: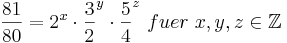 
hat die eindeutige Lösung, als "Tripellogarithmus" bezeichnet: x = -2, y = 4 und z = -1.
Damit gilt für das Intervall i mit dem Frequenzverhältnis 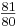die Beziehung 
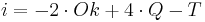. (Siehe synthonisches Komma).
Eine bekannte Orgel, die in reiner Stimmung gestimmt ist, ist die Praetoriusorgel der Universität Freiburg. Um einen Einblick in die Klangwelt der reinen Stimmung zu bekommen findet sich hier eine Aufnahme von dieser Orgel. (Wer noch mehr Aufnahmen wünscht, wird hier fündig)
weiter zur gleichstufig temperierten Stimmung
zurück zur Übersicht
