Quint-System6: Unterschied zwischen den Versionen
(→Der pythagoreische Quintenzirkel) |
(→Der pythagoreische Quintenzirkel) |
||
| Zeile 3: | Zeile 3: | ||
<br><br><div style="text-align:center;"> [[Bild:Pythagoreischer Quintenzirkel.jpg|350px|]] </div><br><br><br> | <br><br><div style="text-align:center;"> [[Bild:Pythagoreischer Quintenzirkel.jpg|350px|]] </div><br><br><br> | ||
| − | Diese Skizze zeigt den pythagoreischen Quintenzirkel und wie sich aus ihm die Töne der pythagoreischen Tonleiter berechnen. Man beginnt bei c und geht immer in Quintabständen nach oben, wobei die Zahlen auf dem Kreis zeigen bei welcher Quinte man sich befindet. Also c-g ist die erste Quinte, g-d die nächste etc. Allerdings soll die Kreisform nicht die Geschlossenheit des Systems ausdrücken, denn der pythagoreische Quintenzirkel schließt sich nicht.<br><br> | + | Diese Skizze zeigt den pythagoreischen Quintenzirkel und wie sich aus ihm die Töne der pythagoreischen Tonleiter berechnen. Man beginnt bei c und geht immer in Quintabständen nach oben, wobei die Zahlen auf dem Kreis zeigen, bei welcher Quinte man sich befindet. Also c-g ist die erste Quinte, g-d die nächste etc. Allerdings soll die Kreisform nicht die Geschlossenheit des Systems ausdrücken, denn der pythagoreische Quintenzirkel schließt sich nicht.<br><br> |
<div style="text-align:center;"> [[Bild:Tonleiterpythagoras.png|700px|]] </div> <br><br> | <div style="text-align:center;"> [[Bild:Tonleiterpythagoras.png|700px|]] </div> <br><br> | ||
Hier ist die pythagoreische C-Dur Tonleiter zu Veranschaulichung graphisch dargestellt.<br> | Hier ist die pythagoreische C-Dur Tonleiter zu Veranschaulichung graphisch dargestellt.<br> | ||
Die oberste Reihe gibt den Schritt zum jeweils nächsten Ton an (großer oder kleiner Schritt).<br> | Die oberste Reihe gibt den Schritt zum jeweils nächsten Ton an (großer oder kleiner Schritt).<br> | ||
| − | Die letzte Reihe das jeweilige Intervall bezogen auf den Grundton.<br><br> | + | Die letzte Reihe das jeweilige Intervall, bezogen auf den Grundton.<br><br> |
| − | "In einer ganzzahligen fortlaufenden Proportion stellt sich dieses Stimmungsprinzip wie folgt | + | "In einer ganzzahligen, fortlaufenden Proportion, stellt sich dieses Stimmungsprinzip wie folgt dar:<br> |
384 : 432 : 486 : 512 : 576 : 648 : 729 : 765 <br> | 384 : 432 : 486 : 512 : 576 : 648 : 729 : 765 <br> | ||
Auf kleinere Verhältniszahlen läßt sich diese Tonleiter nicht reduzieren.“<ref>Schröder S. 51</ref><br> | Auf kleinere Verhältniszahlen läßt sich diese Tonleiter nicht reduzieren.“<ref>Schröder S. 51</ref><br> | ||
| − | Eine fortlaufende Proportion wird immer durch die kleinst | + | Eine fortlaufende Proportion wird immer durch die kleinst möglichen, ganzzahligen Verhältnisse der Frequenzen gebildet. <br> |
„Die pythagoreische Stimmung ist ungeeignet für Modulationen. Und selbst in ihren stärksten Tonarten ist sie für mehrstimmige homophone Musik problematisch. Eine Ursache dafür ist die pythagoreische Terz von 81 : 64 oder 407,820 Cents, die Musiktheoretiker vergangener Epochen mit gutem Grund als Dissonant einstuften.“<ref>Barkowsky S. 7</ref> <br><br> | „Die pythagoreische Stimmung ist ungeeignet für Modulationen. Und selbst in ihren stärksten Tonarten ist sie für mehrstimmige homophone Musik problematisch. Eine Ursache dafür ist die pythagoreische Terz von 81 : 64 oder 407,820 Cents, die Musiktheoretiker vergangener Epochen mit gutem Grund als Dissonant einstuften.“<ref>Barkowsky S. 7</ref> <br><br> | ||
| Zeile 21: | Zeile 21: | ||
# Das pythagoreische Komma: 12 Quinten übertreffen 7 Oktaven (s.o.) | # Das pythagoreische Komma: 12 Quinten übertreffen 7 Oktaven (s.o.) | ||
| − | # Das syntonische Komma: Während des Zusammenspiels eines pythagoreisch gestimmten Saiteninstrument und einem Blasinstrument das Naturtöne spielt, ergibt der Gegensatz zwischen pythagoreischer und reiner Terz eine Disharmonie <math> \textstyle \frac {81}{64}</math> > <math>\textstyle \frac {5}{4};</math> Der Unterschied beträgt <math>\textstyle \frac {81}{80}</math> und wird als syntonisches Komma bezeichnet.Dieses wird in der reinen Stimmung genauer beschrieben | + | # Das syntonische Komma: Während des Zusammenspiels eines pythagoreisch gestimmten Saiteninstrument und einem Blasinstrument, das Naturtöne spielt, ergibt der Gegensatz zwischen pythagoreischer und reiner Terz eine Disharmonie <math> \textstyle \frac {81}{64}</math> > <math>\textstyle \frac {5}{4};</math> Der Unterschied beträgt <math>\textstyle \frac {81}{80}</math> und wird als syntonisches Komma bezeichnet. Dieses wird in der reinen Stimmung genauer beschrieben |
| − | # Die sogenannte „große Diesies“ | + | # Die sogenannte „große Diesies“, eine Reihe von vier kleinen pythagoreischen Terzen, übertrifft die Oktave: <math>(\frac {6}{5})^4 = 2,07 > 2;</math> |
<br><br> | <br><br> | ||
Da seit dem 13. Jahrhundert verstärkt Terzklänge in der Musik auftraten (vorher war die Verwendung der Terz untersagt), und die damit entstehenden Dissonanzen der pythagoreischen Stimmung nicht tragbar waren, musste das Tonsystem also verändert werden.<br> | Da seit dem 13. Jahrhundert verstärkt Terzklänge in der Musik auftraten (vorher war die Verwendung der Terz untersagt), und die damit entstehenden Dissonanzen der pythagoreischen Stimmung nicht tragbar waren, musste das Tonsystem also verändert werden.<br> | ||
Deshalb besann man sich auf die Gedanken von Didmyos (geb. 63 v. Chr.) zurück.<br> | Deshalb besann man sich auf die Gedanken von Didmyos (geb. 63 v. Chr.) zurück.<br> | ||
Er legte das Verhältnis <math>\textstyle \frac {5}{4}</math> für die große Terz fest.<br> | Er legte das Verhältnis <math>\textstyle \frac {5}{4}</math> für die große Terz fest.<br> | ||
| − | Also versuchte man ausgehend von großer Terz, Quinte und Oktave ein neues Tonsystem zu kreieren.<br> | + | Also versuchte man, ausgehend von großer Terz, Quinte und Oktave, ein neues Tonsystem zu kreieren.<br> |
<br> [[Grieninger Sebastian/Facharbeit1/reine Stimmung|weiter zur reinen Stimmung]]<br><br> | <br> [[Grieninger Sebastian/Facharbeit1/reine Stimmung|weiter zur reinen Stimmung]]<br><br> | ||
[[Benutzer:Grieninger_Sebastian/Facharbeit1|zurück zur Übersichtsseite]] | [[Benutzer:Grieninger_Sebastian/Facharbeit1|zurück zur Übersichtsseite]] | ||
---- | ---- | ||
<references /> | <references /> | ||
Version vom 22. Dezember 2010, 21:49 Uhr
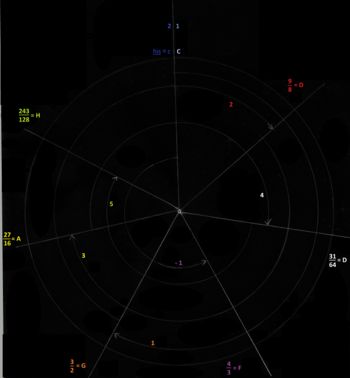
Der pythagoreische Quintenzirkel
Diese Skizze zeigt den pythagoreischen Quintenzirkel und wie sich aus ihm die Töne der pythagoreischen Tonleiter berechnen. Man beginnt bei c und geht immer in Quintabständen nach oben, wobei die Zahlen auf dem Kreis zeigen, bei welcher Quinte man sich befindet. Also c-g ist die erste Quinte, g-d die nächste etc. Allerdings soll die Kreisform nicht die Geschlossenheit des Systems ausdrücken, denn der pythagoreische Quintenzirkel schließt sich nicht.
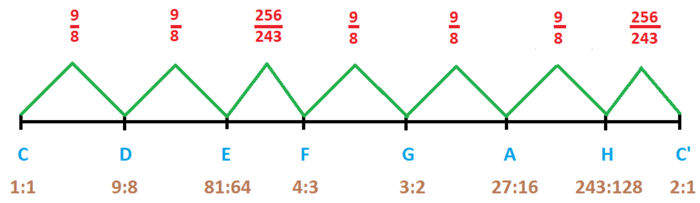
Hier ist die pythagoreische C-Dur Tonleiter zu Veranschaulichung graphisch dargestellt.
Die oberste Reihe gibt den Schritt zum jeweils nächsten Ton an (großer oder kleiner Schritt).
Die letzte Reihe das jeweilige Intervall, bezogen auf den Grundton.
"In einer ganzzahligen, fortlaufenden Proportion, stellt sich dieses Stimmungsprinzip wie folgt dar:
384 : 432 : 486 : 512 : 576 : 648 : 729 : 765
Auf kleinere Verhältniszahlen läßt sich diese Tonleiter nicht reduzieren.“[1]
Eine fortlaufende Proportion wird immer durch die kleinst möglichen, ganzzahligen Verhältnisse der Frequenzen gebildet.
„Die pythagoreische Stimmung ist ungeeignet für Modulationen. Und selbst in ihren stärksten Tonarten ist sie für mehrstimmige homophone Musik problematisch. Eine Ursache dafür ist die pythagoreische Terz von 81 : 64 oder 407,820 Cents, die Musiktheoretiker vergangener Epochen mit gutem Grund als Dissonant einstuften.“[2]
Unstimmigkeiten des pythagoreischen Systems aus musikalischer Sicht:
- Das pythagoreische Komma: 12 Quinten übertreffen 7 Oktaven (s.o.)
- Das syntonische Komma: Während des Zusammenspiels eines pythagoreisch gestimmten Saiteninstrument und einem Blasinstrument, das Naturtöne spielt, ergibt der Gegensatz zwischen pythagoreischer und reiner Terz eine Disharmonie
> 
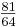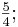Der Unterschied beträgt 
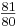und wird als syntonisches Komma bezeichnet. Dieses wird in der reinen Stimmung genauer beschrieben
- Die sogenannte „große Diesies“, eine Reihe von vier kleinen pythagoreischen Terzen, übertrifft die Oktave:
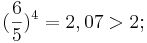
Da seit dem 13. Jahrhundert verstärkt Terzklänge in der Musik auftraten (vorher war die Verwendung der Terz untersagt), und die damit entstehenden Dissonanzen der pythagoreischen Stimmung nicht tragbar waren, musste das Tonsystem also verändert werden.
Deshalb besann man sich auf die Gedanken von Didmyos (geb. 63 v. Chr.) zurück.
Er legte das Verhältnis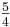 
für die große Terz fest.
Also versuchte man, ausgehend von großer Terz, Quinte und Oktave, ein neues Tonsystem zu kreieren.
weiter zur reinen Stimmung
zurück zur Übersichtsseite
