Einführung der Tonraumzahlen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Einführung der Tonraumzahlen:)
Zeile 6: Zeile 6:
 
<div style="text-align:center;"> 4:8:16:32 </div>
 
<div style="text-align:center;"> 4:8:16:32 </div>
 
Dieser Kette liegt die „fortlaufende“ Proportion 4:8=8:16=16:32 zugrunde (<math>2^n</math> für <math>n \in \N</math>), in der drei Mal des Verhältnis der Oktave (2:1) enthalten ist. Der Tonraum beträgt in diesem Beispiel auch 3 Oktaven.<br>
 
Dieser Kette liegt die „fortlaufende“ Proportion 4:8=8:16=16:32 zugrunde (<math>2^n</math> für <math>n \in \N</math>), in der drei Mal des Verhältnis der Oktave (2:1) enthalten ist. Der Tonraum beträgt in diesem Beispiel auch 3 Oktaven.<br>
−
In dem  Begriff Intervall (lat. Intervallum, Zwischenraum) steckt bereits ein Raumbegriff.<ref>vgl. Bindel S.161</ref><br>
+
In dem  Begriff Intervall (lat. Intervallum, Zwischenraum) steckt bereits ein Raumbegriff.<ref>vgl. Bindel S.161</ref>[[Bild:Gregor Reisch - Margarita Philosophica - Arithmetica.jpg|thumb|]]<br>
−
Die Tonraumzahlen lassen sich, nach Oktavräumen gemessen, in einer Doppelreihe anordnen.<br>
+
Die Tonraumzahlen lassen sich, nach Oktavräumen gemessen, in einer Doppelreihe anordnen.<br>  
  
 
{| class="wikitable"  
 
{| class="wikitable"  

Version vom 20. Dezember 2010, 07:25 Uhr

Einführung der Tonraumzahlen:



In diesem Beispiel soll es zwei Töne A mit der Frequenz 110 Hertz und a' mit der Frequenz 440 Hertz geben. Die beiden Zahlen 110 und 440 lassen sich rein mathematisch auf 3 Arten vergleichen: Man kann zum einen die Differenz (330 Hertz) der beiden Zahlen betrachten, ihr Verhältnis bilden, welches den Wert 1:4 hat, oder über die Zahl 2 die Verhältniskette 1:2:4.
Die Differenz der beiden Frequenzen entspricht einer Differenzton-Bildung, da die beiden Schwingungen von 110 und 440 Hertz miteinander „interferieren“ und dabei ein dritter Ton, mit der Frequenz 330 Hertz entsteht. Der Differenzton von 330 Hertz ist ein e, welches eine Quinte über dem A liegt. Mathematisch kann man das durch die Rechnung 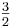\textstyle \frac {3}{2} \cdot 220 Hert z = 330 Hertz nachweisen.
Nehmen wir nun statt dem Verhältnis von 1:4 ein Verhältnis von 4:32, dann ergibt sich folgende Verhältniskette (über die Zahl 2 hinweg):

4:8:16:32

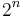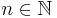Dieser Kette liegt die „fortlaufende“ Proportion 4:8=8:16=16:32 zugrunde (2^n für n \in \N), in der drei Mal des Verhältnis der Oktave (2:1) enthalten ist. Der Tonraum beträgt in diesem Beispiel auch 3 Oktaven.

In dem Begriff Intervall (lat. Intervallum, Zwischenraum) steckt bereits ein Raumbegriff.[1]
Gregor Reisch - Margarita Philosophica - Arithmetica.jpg

Die Tonraumzahlen lassen sich, nach Oktavräumen gemessen, in einer Doppelreihe anordnen.

1 2 4 8 16 Intervallzahlen
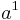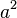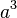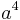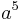a^1 a^2 a^3 a^4 a^5 Ton
0 1 2 3 4 Oktavräume

Wenn man die Doppelreihe über den Anfang hinaus fortführt, folgt analog:

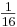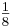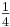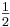\textstyle \frac {1}{16} \textstyle \frac {1}{8} \textstyle \frac {1}{4} \textstyle \frac {1}{2} 1 2 4 8 16 Intervallzahlen
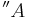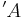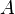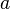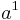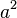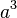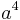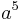''A 'A A a a^1 a^2 a^3 a^4 a^5 Ton
-4 -3 -2 -1 0 1 2 3 4 Oktavräume

Aus dieser Reihe kann man den Logarithmus ablesen, indem man z.B. sagt, dass der Logarithmus zur Zahl 16 zur Basis 2 4 ist. Oder anders ausgedrückt: 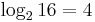\log_2 16 = 4;

Dadurch ergibt sich:


Intervallbezeichnung Intervallzahlen Tonraumzahlen
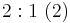
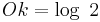
Oktave 2:1 \ (2) Ok = \log \ 2
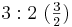
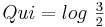
Quinte 3:2 \ (\textstyle \frac{3}{2}) Qui = log \ \textstyle \frac {3}{2}
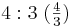
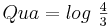
Quarte 4:3 \ (\textstyle \frac {4}{3}) Qua = log \ \textstyle \frac {4}{3}
usw. usw. usw.

Wenn man nun die Intervallzahlen der Tonfolge A – d – a betrachtet, sieht man das auf dem Grundton A das d eine Quarte entfernt ist, und vom d das a wiederum eine Quinte.
Da der Abstand von A zu a eine Oktave beträgt ergibt sich folgende Rechnung:

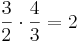
\frac {3}{2} \cdot \frac {4}{3} = 2

Analog folgt die Rechnung für den Tonraum:

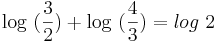
\log \ (\frac {3}{2}) + \log \ (\frac {4}{3}) = log \ 2

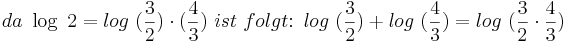
da \ \log \ 2 = log \ (\frac {3}{2}) \cdot (\frac {4}{3}) \ ist \ folgt\colon \ log \ (\frac {3}{2}) + log \ (\frac {4}{3}) = log \ (\frac {3}{2} \cdot \frac {4}{3})

daraus lässt sich die 1. Logarithmusregel ableiten:

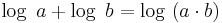
\log \ a + \log \ b = \log \ (a \cdot b)


Die anderen 3 Logarithmusregeln lassen sich ähnlich ableiten.

Wenn man von einem Ton zuerst eine Quinte nach oben geht, und dann wieder eine Quarte nach unten, ergibt sich vom Grundton ein großer Ganztonschritt nach oben:

Intervallzahlen:

Quintintervall geteilt durch Quartintervall ergibt eine große Sekunde
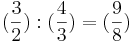
(\frac {3}{2}):(\frac {4}{3}) = (\frac {9}{8})



Tonraum:

Quintraum minus Quartraum ergibt einen großen Sekundschritt(raum)
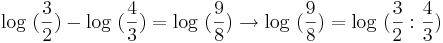
\log \ (\frac {3}{2}) - \log \ (\frac {4}{3}) = \log \ (\frac {9}{8}) \to \log \ (\frac {9}{8}) = \log \ (\frac {3}{2} : \frac {4}{3})
daher gilt: 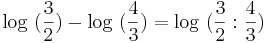\log \ (\frac {3}{2}) - \log \ (\frac {4}{3}) = \log \ (\frac {3}{2} : \frac {4}{3})



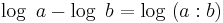
und weiter: \log \ a - \log \ b = \log \ ( a : b )


Nun geht man von einem Grundton eine Quinte aufwärts, und schließlich nochmals eine Quinte aufwärts. Das Ergebnis ist eine None (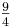\textstyle \frac {9}{4})

Intervallzahlen:

Quintintervall mal Quintintervall = Nonenintervall
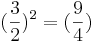
(\frac {3}{2})^2 = (\frac {9}{4})



Tonraum:

Quintenraum plus Quintenraum = Nonenraum
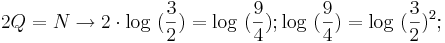
2Q = N \to 2 \cdot \log \ (\frac {3}{2}) = \log \ (\frac {9}{4}); \log \ (\frac {9}{4}) = \log \ (\frac {3}{2})^2;


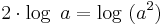
daraus folgt: 2 \cdot \log \ a = \log \ (a^2)


Zuletzt halbiert man den Nonenraum A-h und landet bei der Quinte zu A, nämlich e.

Intervallzahlen:

eine halbe None = Quinte
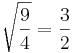
\sqrt {\frac {9}{4}} = \frac {3}{2}



Tonraum:

halbierter Nonenraum = Quintraum
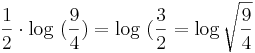
\frac {1}{2} \cdot \log \ (\frac {9}{4}) = \log \ (\frac {3}{2} = \log \sqrt {\frac {9}{4}}


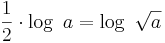
daraus folgt: \frac {1}{2} \cdot \log \ a = \log \ \sqrt{a}


Damit sind alle 4 Rechenregeln des Logarithmus für die Tonraumrechnung gezeigt.

weiter zum Beweis der Logarithmusregeln
weiter zum Cent-System

zurück zur Übersichtsseite

  1. ↑ vgl. Bindel S.161
Von „http://rmg.zum.de/index.php?title=Benutzer:Grieninger_Sebastian/Facharbeit/Einführung_der_Tonraumzahlen&oldid=39329“