Quint-System4: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Berechnung der Intervalle in der pythagoreischen Stimmung)
(→‎Berechnung der Intervalle in der pythagoreischen Stimmung)
Zeile 24: Zeile 24:
 
16:9 semiditonus et diapente (kleine Septime)<br>
 
16:9 semiditonus et diapente (kleine Septime)<br>
 
243:128         ditonus et diapente (große Septime)<br>
 
243:128         ditonus et diapente (große Septime)<br>
−
2:1 diapason (Oktave)“<br>
+
2:1 diapason (Oktave)“<ref>Münxelhaus S. 111</ref><br>
  
 
[[Benutzer:Grieninger_Sebastian/Facharbeit/Quint-System5| ''' weiter zum pythagoreischen Komma''']]<br><br>
 
[[Benutzer:Grieninger_Sebastian/Facharbeit/Quint-System5| ''' weiter zum pythagoreischen Komma''']]<br><br>
 
[[Benutzer:Grieninger_Sebastian/Facharbeit|zurück zur Übersichtsseite]]
 
[[Benutzer:Grieninger_Sebastian/Facharbeit|zurück zur Übersichtsseite]]
 +
----
 +
<references />

Version vom 20. Dezember 2010, 05:23 Uhr

Berechnung der Intervalle in der pythagoreischen Stimmung



Man kann alle Töne nach der auf der auf der vorgehenden Seite angegebenen Formel berechnen. Aus den verschiedenen Tonhöhen enthält man die verschiedenen Intervalle.
Die pythagoreische Stimmung setzt sich aus fünf großen und zwei kleinen Tonschritten zusammen. Den großen Tonschritt haben wir bereits berechnet.

Er beträgt 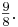\textstyle \frac {9}{8}.

Alternativ kann man ihn berechnen, wenn man von einer Quinte eine Quarte abzieht:

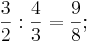
\frac {3}{2} : \frac {4}{3} = \frac {9}{8};

Der kleine Tonschritt, der Halbton ergibt sich, wenn man von der Quarte zwei Ganztöne „abzieht“

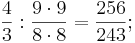
\frac {4}{3}: \frac {9\cdot9}{8\cdot8} = \frac {256}{243};

„In der folgenden Übersicht über die Intervalle der pythagoreischen Skala mit den entsprechenden mittelalterlichen Bezeichnungen sind die Zahlenverhältnisse vom Halbton bis zu Oktave zusammengestellt:

256 : 243 semitonium (Halbton)
9 : 8 tonus (Ganzton)
32 : 27 semiditonus (kleine Terz)
81 : 64 ditonus (große Terz)
4 : 3 diatessaron (Quarte)
729 : 512 tritonus (Tritonus)
3 : 2 diapente (Quinte)
128 : 81 semitonium et diapente (kleine Sexte)
27:16 tonus et diapente (große Sexte)
16:9 semiditonus et diapente (kleine Septime)
243:128 ditonus et diapente (große Septime)
2:1 diapason (Oktave)“[1]

weiter zum pythagoreischen Komma

zurück zur Übersichtsseite

  1. ↑ Münxelhaus S. 111
Von „http://rmg.zum.de/index.php?title=Benutzer:Grieninger_Sebastian/Facharbeit/Quint-System4&oldid=39318“