Q12 Mathematik: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 6: Zeile 6:
 
<tr><td  width="800px" valign="top">
 
<tr><td  width="800px" valign="top">
  
−
==== 1. Das Flächenproblem ====
+
===1. Integralrechnung ===
  
 +
;Das Flächenproblem
 
{|
 
{|
 
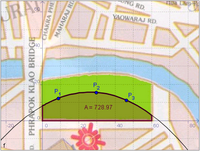
|[[Bild:Integral Grundstück.png|200px|left]]
 
|[[Bild:Integral Grundstück.png|200px|left]]
Zeile 16: Zeile 17:
  
  
−
==== 2. Unter- und Obersumme ====
+
;Unter- und Obersumme  
 
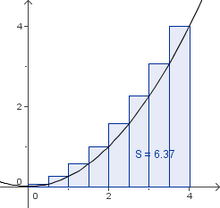
[[bild:Int_abb1.png|220px|right]]
 
[[bild:Int_abb1.png|220px|right]]
 
*Begriffsklärung [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/unterobersumme.htm Unter- und Obersumme]
 
*Begriffsklärung [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/unterobersumme.htm Unter- und Obersumme]
Zeile 42: Zeile 43:
  
  
−
====3. Integralfunktion====
+
;Integralfunktion
  
 
*[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/integralfkt/integralfkt2.html Veranschaulichung durch GeoGebra-Applet]
 
*[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/integralfkt/integralfkt2.html Veranschaulichung durch GeoGebra-Applet]
  
  
−
==== 4. [[Q12 Mathematik/Hausaufgaben|Hausaufgaben]] ====
+
 
 +
</td></tr></table></center>
 +
 
 +
 
 +
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 +
<tr><td  width="800px" valign="top">
 +
=== 2. Binomialverteilung===
 +
 
 +
 
 +
</td></tr></table></center>
 +
 
 +
 
 +
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 +
<tr><td  width="800px" valign="top">
 +
=== [[Q12 Mathematik/Hausaufgaben|Hausaufgaben]] ===
 
</td></tr></table></center>
 
</td></tr></table></center>
  

Version vom 11. Dezember 2010, 19:33 Uhr


1. Integralrechnung

Das Flächenproblem
Integral Grundstück.png
 Ziel der folgenden Überlegungen ist es, ein Verfahren zu entwickeln, mit dem Flächeninhalte von krummlinig begrenzten Flächen berechnet werden können.


Unter- und Obersumme
Int abb1.png
  1. Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
  2. Berechne die zugehörige Ober- und Untersumme.
  3. Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
  4. Lösung:
  • Berechnung von Unter- und Obersummen mit GeoGebra


Integralfunktion



2. Binomialverteilung


Hausaufgaben

Achtung: Die Seiten öffnen sich teilweise sehr langsam!
Kapitel aus dem Buch: Kapitel 2
Lösungen: Kapitel 1 - Kapitel 2 - Kapitel 3
Von „http://rmg.zum.de/index.php?title=Q12_Mathematik&oldid=38445“