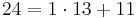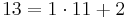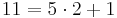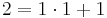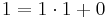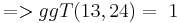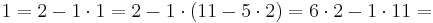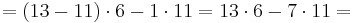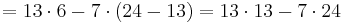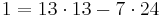Mathematische Grundlagen 3: Unterschied zwischen den Versionen
| Zeile 124: | Zeile 124: | ||
</popup> | </popup> | ||
<br> | <br> | ||
| − | [[Benutzer:Deininger_Matthias/Facharbeit/RSA-Algorithmus| ''' | + | [[Bild:Weiter.png|weiter]] [[Benutzer:Deininger_Matthias/Facharbeit/RSA-Algorithmus| '''weiter zum RSA-Algorithmus''']] |
<br> | <br> | ||
<br> | <br> | ||
Version vom 11. Dezember 2010, 12:00 Uhr
Modulare Inverse
In der 6. Klasse hast du dich schon einmal mit Kehrwerten beschäftigt. Bei der Zahl 2 ist der Kehrwert bezüglich der Multiplikation 0,5. 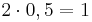 , den Kehrwert kann man auch als Inverse bezeichnen. Im Folgenden gilt es zu untersuchen, ob auch modulare Inversen existieren und wenn ja unter welchen Bedingungen, wenn wir nur ganzzahlige Inverse betrachten möchten.
Aus den Angaben von Alice folgt:
, den Kehrwert kann man auch als Inverse bezeichnen. Im Folgenden gilt es zu untersuchen, ob auch modulare Inversen existieren und wenn ja unter welchen Bedingungen, wenn wir nur ganzzahlige Inverse betrachten möchten.
Aus den Angaben von Alice folgt: 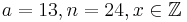 Wie für den Kehrwert, so gilt auch für die modulare Inverse, dass das Resultat 1 ergeben muss.
Wie für den Kehrwert, so gilt auch für die modulare Inverse, dass das Resultat 1 ergeben muss.
| Allgemein gilt also: | Alternative Schreibweise für die modulare Inverse: |
|---|---|
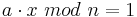 |
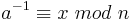 |
Diese Gleichungen sind äquivalent zu:
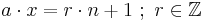 diese Schreibweise erinnert an Lemma 1.4, wonach man vermuten kann, dass die Gleichung nur für ggT(a,n)=1 gilt.
diese Schreibweise erinnert an Lemma 1.4, wonach man vermuten kann, dass die Gleichung nur für ggT(a,n)=1 gilt.
Für die Aufgabe von Alice gilt somit:
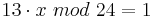
Falls eine Lösung existiert, soll nun eine ganze Zahl x gefunden werden, so dass die Gleichung erfüllt ist.
Wie du anhand von Alices Beispiel selbst überprüfen kannst, ist dies bereits bei so kleinen Zahlen ziemlich schwierig.
Deshalb betrachten wir nun den Satz von der modularen Inversen und werden darauf einen Algorithmus kennen lernen, mithilfe dessen sich die modulo Inverse, die auch als multiplikative Inverse bezeichnet werden kann, relativ einfach berechnen lässt.
Satz 2.3[1] (Satz von der modularen Inversen) Es sei 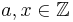 und
und 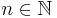 mit ggT(a,n)=1, so ist x die modulare Inverse zu a, wenn gilt:
mit ggT(a,n)=1, so ist x die modulare Inverse zu a, wenn gilt:
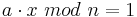
Beweis: Da gilt ggT(a,n)=1, gibt es ganze Zahlen x und y mit folgenden Eigenschaften:
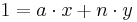
da ny durch n teilbar ist, ergibt ax bei Division durch n den Rest 1, also ist
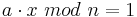
Folglich gibt es immer eine eindeutige modulare Inverse, wenn gilt ggT(a,n)=1 □
Wie du bereits aus Abschnitt 1 weißt, lässt sich der ggT zweier Zahlen mithilfe des Euklidischen Algorithmus bestimmen.
Algorithmus 2.4[1] (Berechnung der modularen Inverse)
Es seien 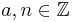 mit ggT(a,n) = 1.
Man berechne zunächst die Vielfachsummendarstellung
mit ggT(a,n) = 1.
Man berechne zunächst die Vielfachsummendarstellung 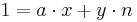 . Dann ist x die modulare Inverse von a modulo n.
. Dann ist x die modulare Inverse von a modulo n.
Bei den, von Alice gewählten, Zahlen gilt ggT(13,24)=1, also existiert eine modulare Inverse, da 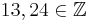 , lässt sich obiger Algorithmus hier anwenden, um die modulare Inverse zu 13 mod 24 zu bestimmen.
, lässt sich obiger Algorithmus hier anwenden, um die modulare Inverse zu 13 mod 24 zu bestimmen.
Gesucht sind x und y, für 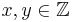
1 = 13x + 24y
Bestimme mithilfe des Euklidischen Algorithmus die Vielfachsummendarstellung von 13 und 24 und ermittle daraus die modulare Inverse zu 13 mod 24.
Alice beschäftigt sich jetzt mit dem Satz von Fermat, sowie dem Satz von Euler, weil sie gelesen hat, dass diese Sätze elementar für das RSA-Kryptosystem sind. Folglich solltest auch du diese beiden Sätze kennen lernen, bevor du dich dem RSA-Kryptosystem zuwendest.
Kleiner Satz von Fermat
Satz 2.5[2] (Der kleine Satz von Fermat) Es sei p eine Primzahl, so gilt für alle 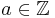 mit ggT(a,p)=1.
mit ggT(a,p)=1.
Beweis: (durch Betrachtung der Äquivalenzklassen/Restklassenrepräsentanten)
Die möglichen Reste ungleich 0 bei Division einer ganzen Zahl durch p sind 1,2,3, ... ,p-1. Die Zahlen 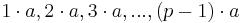 sind ebenfalls (p-1) verschiedene Zahlen; je zwei von ihnen haben verschiedene Reste (ungleich 0) mod p, da wegen ggT(a,p) = 1 gilt:
sind ebenfalls (p-1) verschiedene Zahlen; je zwei von ihnen haben verschiedene Reste (ungleich 0) mod p, da wegen ggT(a,p) = 1 gilt:
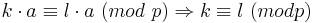 ,
was wegen der Größe dieser Zahlen nur für k = l möglich ist. Also ist jede der Zahlen
,
was wegen der Größe dieser Zahlen nur für k = l möglich ist. Also ist jede der Zahlen 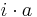 kongruent zu genau einem Element aus {1,2,3, ... ,p-1} und es gilt:
kongruent zu genau einem Element aus {1,2,3, ... ,p-1} und es gilt:
![[1\cdot a], [2\cdot a], [3\cdot a], ..., [(p-1)\cdot a] = [1],[2],[3],..., [p-1] d.h.](/images/math/1/b/f/1bfde9c09eee176ba8429a03e6569cb8.png)
![\{(1\cdot 2\cdot 3\cdot ...\cdot (p-1)) \cdot a^{p-1}\} \equiv \{1\cdot 2\cdot 3\cdot ... \cdot (p-1)]\}\ (mod\ p)](/images/math/4/a/2/4a27167b32a7b907d0f1c4cb17575c52.png)
Hieraus folgt durch Division: 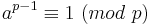 □
□
Alice wählt sich p = 5 und a = 4, um den Satz zu testen.
Somit gilt nach dem kleinen Satz von Fermat:
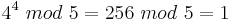
Beim Satz von Fermat handelt es sich lediglich um einen Sonderfall des Satzes von Euler:
Satz von Euler
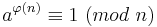
Hierbei bezeichnet 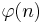 die Anzahl der zu n teilerfremden Zahlen aus der Menge {1,2,...,n-1}. Wenn p eine Primzahl ist, so gilt:
die Anzahl der zu n teilerfremden Zahlen aus der Menge {1,2,...,n-1}. Wenn p eine Primzahl ist, so gilt: 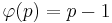 , für zwei voneinander verschiedene Primzahlen p,q gilt folglich:
, für zwei voneinander verschiedene Primzahlen p,q gilt folglich: 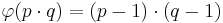
![]() weiter zum RSA-Algorithmus
weiter zum RSA-Algorithmus
zurück zur Übersicht