Multiplizieren und Dividieren von Summen und Differenzen: Unterschied zwischen den Versionen
K (→Ausmultiplizieren und Ausklammern) |
K (→Ausmultiplizieren und Ausklammern) |
||
| Zeile 193: | Zeile 193: | ||
<br /> | <br /> | ||
<div style="orange:0px; margin-right:90px; border: solid orange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: red">Erklärung:</span>''' | <div style="orange:0px; margin-right:90px; border: solid orange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: red">Erklärung:</span>''' | ||
| − | Enthält in einer Summe aus Produkten jedes Produkt einen oder mehrere '''gemeinsame''' Faktoren, so kann man diese nach dem Distributivgesetz ausklammern. Dieser Rechenschritt verwandelt eine <u>Summe in ein Produkt</u>. | + | {|width="99%" |
| + | |width="100%" style="vertical-align:top"| | ||
| + | Enthält in einer Summe aus Produkten jedes Produkt einen oder mehrere '''gemeinsame''' Faktoren, so kann man diese nach dem Distributivgesetz ausklammern. | ||
| + | <br />Dieser Rechenschritt verwandelt eine <u>Summe in ein Produkt</u>. | ||
: a•b + a•c + a•d + a•e = a•(b+c+d+e) | : a•b + a•c + a•d + a•e = a•(b+c+d+e) | ||
| + | |width="50%" style="vertical-align:top"| | ||
| + | |width="70%" style="vertical-align:center"| | ||
| + | [[Bild:erklärwurm.gif]] | ||
| + | |} | ||
</div> | </div> | ||
<br /> | <br /> | ||
Version vom 25. November 2010, 11:25 Uhr
Inhaltsverzeichnis |
Multiplizieren und Dividieren von Summen und Differenzen
Distributivgesetz der Multiplikation
|
Überlege nun, wie du das Produkt in eine Summe umwandeln kannst.
|
Man multipliziert eine Summe (bzw. Differenz) mit einem Faktor, indem man jedes Glied der Summe (bzw. Differenz) mit dem Faktor multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert).
|
Beispiel:
(2-y)•3 = 2•3-y•3 = 6-3y
Multipliziere nun folgende Terme aus:
- (4+m)•2
- (7+z)•(-4)
- (
 +a)•
+a)•
- (
 -k)•
-k)•
Distributivgesetz der Division
Anna, Sara und Kerstin haben eine Tüte Bonbons geschenkt bekommen. Die Tüte enthält 9 Waldbeerbonbons und 18 Kirschbonbons. Die drei Freundinnen wollen die Bonbons gerecht untereinander aufteilen. Jede macht einen Vorschlag:
Was meinst du? Schreibe die beiden Rechenvorschriften zu Termen um und prüfe, welche der drei Mädchen recht hat. |
Versuche nun, eine dafür allgemein geltende Rechenregel zu formulieren.
|
Man dividiert eine Summe (oder Differenz) durch einen von null verschiedenen Divisor, indem man jeder Glied der einen Summe (bzw. Differenz) durch den Divisor teilt und die entstandenen Quotienten addiert (bzw. subtrahiert).
bzw.:(a+b):c = a:c + b:c für a, b,
bzw.: (a-b):c = a:c - b:c für a, b,
|
Beispiel:
(a+6):8 = 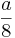 +
+  =
= 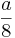 +
+
Dividiere selbst:
- (z-0,5):2
- (m-c):c
- (2,8-0,3):a
Ausmultiplizieren und Ausklammern
|
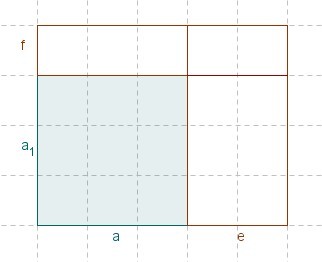
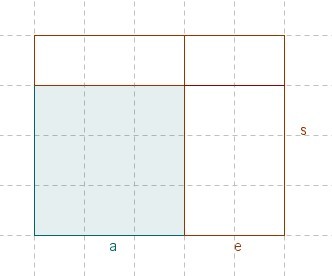
Du hast vorhin ein Quadrat berechnet, dessen Seitenlänge a um e erweitert wurde und dessen andere Seitenlänge zu s erweitert wurde. Berechne jetzt den Flächeninhalt für das Rechteck, wenn sich s aus a und f zusammensetzt. (siehe Skizze) |
Mit Hilfe des Distributivgesetzes kannst du eine Summe mit einem Faktor multiplizieren (bzw. dividieren). Überlege, wie der neue Term für den Flächeninhalt AF = (a+e)•(a+f) ausmultipliziert werden kann.
|
Man multipliziert zwei Summen (bzw. Differenzen) miteinander, indem man jedes Glied der einen Summe (bzw. Differenz) mit jedem Glied der anderen Summe (bzw. Differenz) multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert). Dieser Rechenschritt verwandelt ein Produkt in eine Summe.
|
Beispiel:
(x+2)(x+5) = x(x+5) + 2(x+5) = (x2+5x) + (2x+10) = x2 +5x +2x +10 = x2+7x+10
Berechne selbst:
- (y+7)(3+y)
- (a-5)(1+a+2)
- (m+n+o)(m-n-o)
Aufgabenstellung:
Wende das Distributivgesetz an, um aus einer Summe ein Produkt zu machen.
21x+14y+7
|
Enthält in einer Summe aus Produkten jedes Produkt einen oder mehrere gemeinsame Faktoren, so kann man diese nach dem Distributivgesetz ausklammern.
|
Beispiel:
2a-2b = 2(a-b)
Berechne selbst:
- ax+a
- 6z2+21z
- 6ab3+9ab2-15ab
Übungsaufgaben
Multipliziere aus und fasse zusammen
- (m-n)(5n+m)
- (2a-3b)(2a-3b)
- (5r+2)(3r+2)
Berechne den Flächeninhalt aus den angegebenen Maßen und vereinfache dann so weit wie möglich.
Die Terme in der ersten Zeile sind jeweils vereinfachte Produkte aus 2 der Termen, die unten stehen. Finde diese Terme und ziehe sie mit der Maus in das Lösungsfeld.
| x2 +5x+6 | x2 -4x+3 | x2-3x-10 | x2+2x-8 | x2 +1 | x2+4x+4 |
| x+2 | x-3 | x-5 | x+4 | x-1 | x+2 |
| x+3 | x-1 | x+2 | x-2 | x+1 | x+2 |

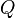

 +
+ 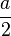
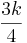

 (9+18):3 = 9:3 + 18:3 = 9
(9+18):3 = 9:3 + 18:3 = 9
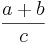 =
= 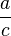 +
+ 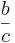 für a, b,
für a, b, 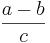 =
= 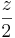 -
- 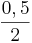 =
= 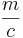 -
-  =
=