Mathematische Grundlagen: Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
Beweis: Es wird zunächst gezeigt, dass sich jede natürliche Zahl n > 1 als Produkt von Primfaktoren schreiben lässt. Falls n prim ist, ist die Zerlegung gezeigt. Andernfalls besitzt sie einen Teiler d > 1 und es ist <math>d\cdot\frac{n}{d}</math> eine Zerlegung von n in echt kleiner positive ganze Zahlen d und <math>\frac{n}{d}</math>. Falls beide prim sind, so ist die Zerlegung beendet. Im anderen Fall lassen sich sich diese wieder zerlegen und so weiter. Da bei diesem Prozess die Faktoren immer kleiner werden, aber positiv bleiben, muss dieser Prozess irgendwann abbrechen und wir besitzen eine Zerlegung in Primfaktoren.<br> | Beweis: Es wird zunächst gezeigt, dass sich jede natürliche Zahl n > 1 als Produkt von Primfaktoren schreiben lässt. Falls n prim ist, ist die Zerlegung gezeigt. Andernfalls besitzt sie einen Teiler d > 1 und es ist <math>d\cdot\frac{n}{d}</math> eine Zerlegung von n in echt kleiner positive ganze Zahlen d und <math>\frac{n}{d}</math>. Falls beide prim sind, so ist die Zerlegung beendet. Im anderen Fall lassen sich sich diese wieder zerlegen und so weiter. Da bei diesem Prozess die Faktoren immer kleiner werden, aber positiv bleiben, muss dieser Prozess irgendwann abbrechen und wir besitzen eine Zerlegung in Primfaktoren.<br> | ||
Zur Eindeutigkeit: Angenommen, man hat zu einer Zahl n zwei Zerlegungen | Zur Eindeutigkeit: Angenommen, man hat zu einer Zahl n zwei Zerlegungen | ||
| − | <math>p_1\cdot p_2\cdot...\cdot p_l=q_1\cdot q_2\cdot...\cdot q_k</math> in Primfaktoren <math>p_r,\ q_r</math>, so | + | <math>p_1\cdot p_2\cdot...\cdot p_l=q_1\cdot q_2\cdot...\cdot q_k</math> in Primfaktoren <math>p_r,\ q_r</math>, so das gilt <math>l,k,r\in \N</math>.(Hierbei können Zahlen natürlich auch mehrfach vorkommen.) Man stelle sich vor, man hätte bereits alle gleichen Elemente auf beiden Seiten herausgekürzt. Dann sind alle <math>p_r</math> von allen <math>q_r</math> verschieden. Dies steht aber im Widerspruch dazu, dass dies alles Primelemente sind. Da nämlich z.B. <math>p_1</math>, die rechte Seite teilt, so muss <math>p_1</math>, da es eine Primzahl ist, eine der Zahlen <math> q_r </math> teilen. Da diese aber selbst Primzahlen sind, würde <math>p_1</math> mit dieser übereinstimmen. Widerspruch.[[Benutzer:Deininger_Matthias/Facharbeit/Quod_erat_demonstrandum| □ ]] |
</popup> | </popup> | ||
<br> | <br> | ||
| Zeile 34: | Zeile 34: | ||
Es gibt eine effizientere Methode, als die Primfaktorzerlegung, um den ggT zweier natürlicher Zahlen zu bestimmen und damit die Punktzahl von Alice zu ermitteln. Diese Methode wird als Euklidischer Algorithmus bezeichnet, weil er ca. 300 v. Chr. von Euklid in seinem Buch „Elemente“ beschrieben wurde. Historiker vermuten jedoch, dass Euklid den Algorithmus nicht selbst entdeckt hat und schätzen die Entstehungszeit auf ca. 500 v. Chr.<br> | Es gibt eine effizientere Methode, als die Primfaktorzerlegung, um den ggT zweier natürlicher Zahlen zu bestimmen und damit die Punktzahl von Alice zu ermitteln. Diese Methode wird als Euklidischer Algorithmus bezeichnet, weil er ca. 300 v. Chr. von Euklid in seinem Buch „Elemente“ beschrieben wurde. Historiker vermuten jedoch, dass Euklid den Algorithmus nicht selbst entdeckt hat und schätzen die Entstehungszeit auf ca. 500 v. Chr.<br> | ||
Der Algorithmus beruht auf Division mit Rest.<br> | Der Algorithmus beruht auf Division mit Rest.<br> | ||
| + | <br> | ||
| + | '''Algorithmus 1.2''' (Euklidischer Algorithmus) Es seien <math>a,b \in \N</math>. Man bestimmt <math>q,r \in \N_0</math>, so dass gilt: | ||
| + | |||
| + | <div style = "marign: auto;"><math>a\ =\ b\cdot p + r\ und\ 0\le r < b</math></div> | ||
| + | |||
| + | Dann gilt ggT(a,b) =ggT(b,r).<br> | ||
| + | Anschließend wendet man das Verfahren auf b und r an. Dies führt man so lange fort, bis man den ggT direkt bestimmen kann. | ||
Version vom 2. September 2010, 15:19 Uhr
Aber nun zu den mathematischen Grundlagen, die für RSA relevant sind.
Aufgabe:
Alice möchte Bob die Punktzahl ihrer letzten Matheklausur übersenden. Da sie nun weiß, dass ein Unbekannter ihre Nachrichten liest, versucht sie die Information so zu übersenden, dass Mallory die Punktzahl nicht herausfindet. Weil sie noch kein Verschlüsselungsverfahren einsetzt, versucht sie es wie folgt:
„Meine Punktzahl ist der größte gemeinsame Teiler der Zahlen 90 und 105.“
Und es funktioniert tatsächlich, Mallory, der Mathe immer gehasst hat, erkennt nicht, welche Punktzahl Alice erreicht hat.
Kannst du die Punktzahl von Alice ermitteln?
Den größten gemeinsamen Teiler (ggT) von natürlichen Zahlen hast du bereits in der 5.Klasse berechnet. Dazu hast du, wie in obigem Beispiel, Zahlen in ihre Primfaktoren zerlegt und daraus anschließend den ggT ermittelt. Das es zu jeder natürlichen Zahl n eine eindeutige Primfaktorzerlegung gibt, zeigt folgender Satz:
Satz 1.0 (Fundamentalsatz der elementaren Zahlentheorie oder Satz über die eindeutige Primfaktorzerlegung)
Jede natürliche Zahl n > 1 lässt sich auf eindeutige Weise in ein Produkt von Primfaktoren zerlegen.
Der größte gemeinsame Teiler ist allgemein wie folgt definiert:
Definition 1.1 Es seien 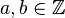 . Die größte natürliche Zahl, die sowohl a als auch b teilt, heißt größter gemeinsamer Teiler und wird mit ggT(a,b) bezeichnet.
. Die größte natürliche Zahl, die sowohl a als auch b teilt, heißt größter gemeinsamer Teiler und wird mit ggT(a,b) bezeichnet.
Es gibt eine effizientere Methode, als die Primfaktorzerlegung, um den ggT zweier natürlicher Zahlen zu bestimmen und damit die Punktzahl von Alice zu ermitteln. Diese Methode wird als Euklidischer Algorithmus bezeichnet, weil er ca. 300 v. Chr. von Euklid in seinem Buch „Elemente“ beschrieben wurde. Historiker vermuten jedoch, dass Euklid den Algorithmus nicht selbst entdeckt hat und schätzen die Entstehungszeit auf ca. 500 v. Chr.
Der Algorithmus beruht auf Division mit Rest.
Algorithmus 1.2 (Euklidischer Algorithmus) Es seien 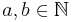 . Man bestimmt
. Man bestimmt 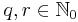 , so dass gilt:
, so dass gilt:
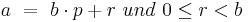
Dann gilt ggT(a,b) =ggT(b,r).
Anschließend wendet man das Verfahren auf b und r an. Dies führt man so lange fort, bis man den ggT direkt bestimmen kann.
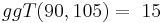
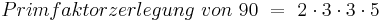
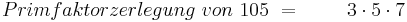
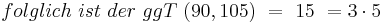
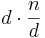 eine Zerlegung von n in echt kleiner positive ganze Zahlen d und
eine Zerlegung von n in echt kleiner positive ganze Zahlen d und 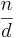 . Falls beide prim sind, so ist die Zerlegung beendet. Im anderen Fall lassen sich sich diese wieder zerlegen und so weiter. Da bei diesem Prozess die Faktoren immer kleiner werden, aber positiv bleiben, muss dieser Prozess irgendwann abbrechen und wir besitzen eine Zerlegung in Primfaktoren.
. Falls beide prim sind, so ist die Zerlegung beendet. Im anderen Fall lassen sich sich diese wieder zerlegen und so weiter. Da bei diesem Prozess die Faktoren immer kleiner werden, aber positiv bleiben, muss dieser Prozess irgendwann abbrechen und wir besitzen eine Zerlegung in Primfaktoren.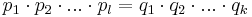 in Primfaktoren
in Primfaktoren 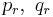 , so das gilt
, so das gilt 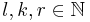 .(Hierbei können Zahlen natürlich auch mehrfach vorkommen.) Man stelle sich vor, man hätte bereits alle gleichen Elemente auf beiden Seiten herausgekürzt. Dann sind alle
.(Hierbei können Zahlen natürlich auch mehrfach vorkommen.) Man stelle sich vor, man hätte bereits alle gleichen Elemente auf beiden Seiten herausgekürzt. Dann sind alle 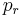 von allen
von allen 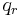 verschieden. Dies steht aber im Widerspruch dazu, dass dies alles Primelemente sind. Da nämlich z.B.
verschieden. Dies steht aber im Widerspruch dazu, dass dies alles Primelemente sind. Da nämlich z.B. 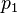 , die rechte Seite teilt, so muss
, die rechte Seite teilt, so muss 
