Auflösen von Klammern: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (→Übungsaufgaben) |
K (→Übungsaufgaben) |
||
| Zeile 33: | Zeile 33: | ||
<br /><br /> | <br /><br /> | ||
==<span style="color: green">Übungsaufgaben</span> == | ==<span style="color: green">Übungsaufgaben</span> == | ||
| − | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>'''Vereinfache so | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>'''Vereinfache so weit wie möglich: |
* 36a-(12-+9) | * 36a-(12-+9) | ||
Version vom 23. August 2010, 13:49 Uhr
Auflösen von Klammern
Klammerregeln bei Addition und Subtraktion
Überlege, wie du die Klammern auflösen kannst.
- T(x;y)= 9x+(8x+5y)
- T(x;y)= 9x+(8x-5y)
- T(x;y)= 9x-(8x+5y)
- T(x;y)= 9x-(8x-5y)
Erklärung:
Steht vor der Klammer ein Pluszeichen, so kann man die Klammer weglassen, ohne dass sich der Wert des Terms ändert.
Steht vor der Klammer ein Pluszeichen, so kann man die Klammer weglassen, ohne dass sich der Wert des Terms ändert.
- a+(b+c) = a+b+c
- a+(b-c) = a+b-c
Steht vor der Klammer ein Minuszeichen, so wird beim Auflösen der Klammer aus jedem Pluszeichen in der Klammer ein Minuszeichen und aus jedem Minuszeichen in der Klammer ein Pluszeichen.
- a-(b+c) = a-b-c
- a-(b-c) = a-b+c
Übungsaufgaben
Aufgabe 1:Vereinfache so weit wie möglich:
- 36a-(12-+9)
- 27n+(-5n+4)
- 29m-(3-m)
- 8x+(9-x)
Aufgabe 2:
- Schreibe die Summe (a-b)+(x-y) als Differenz
- Schreibe die Differenz (m-l)-(z-u) als Summe
Aufgabe 3:
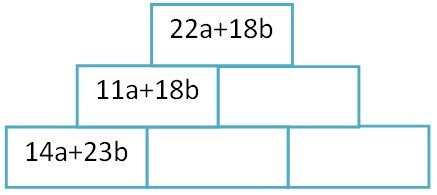
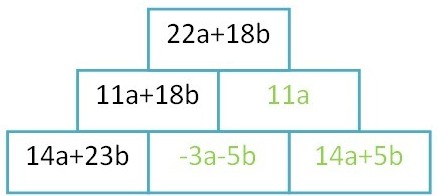
Finde die fehlenden Zeichen (O) und Termglieder(
)
- (n +2y) - (4n O 17y) = 6n+19y
- (2n O 3m) + (n - m) = 7n-10m
- (13a O b) - (a+5b) = 4a+4b
Aufgabe 4:
|
|
