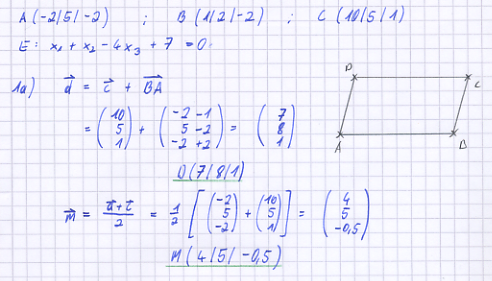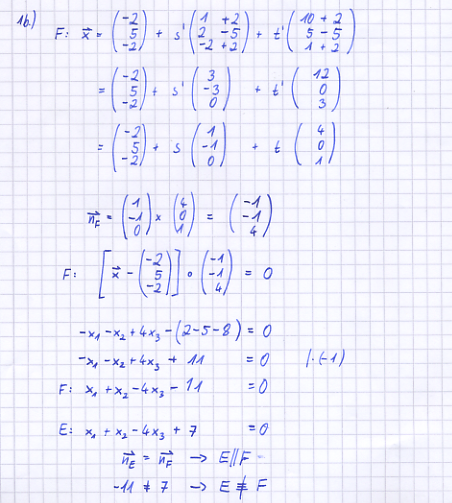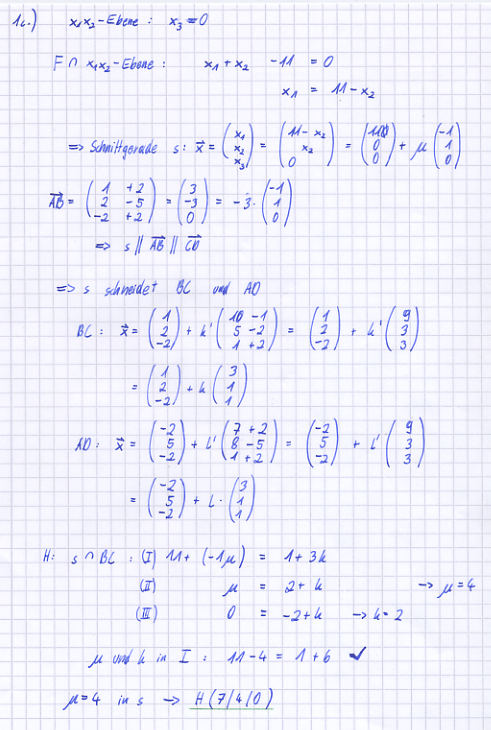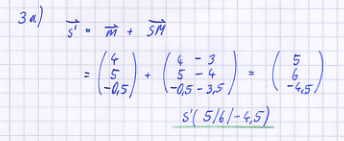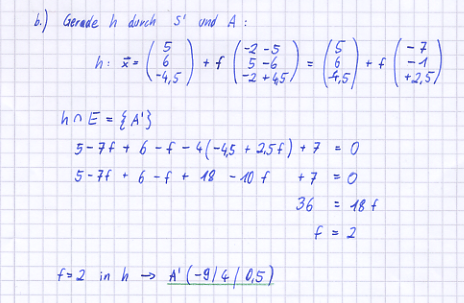2004 V: Unterschied zwischen den Versionen
| Zeile 65: | Zeile 65: | ||
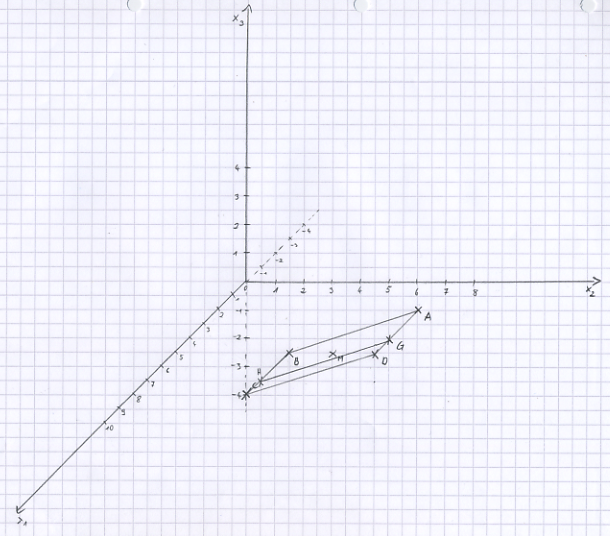
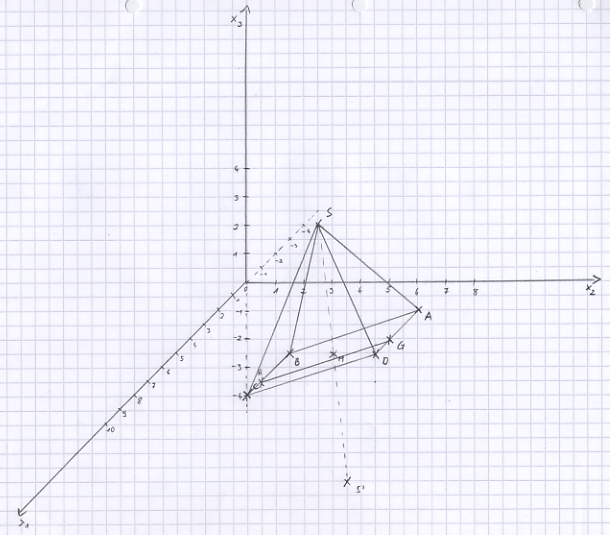
c) Die Parallelogrammfläche schneidet die x<sub>1</sub>x<sub>2</sub>-Ebene in der Strecke [GH]. Berechnen Sie die Koordinaten der Punkte der Punkte G und H und tragen Sie die Strecke [GH] in die angelegte Zeichnung ein. | c) Die Parallelogrammfläche schneidet die x<sub>1</sub>x<sub>2</sub>-Ebene in der Strecke [GH]. Berechnen Sie die Koordinaten der Punkte der Punkte G und H und tragen Sie die Strecke [GH] in die angelegte Zeichnung ein. | ||
| − | [Zur Kontrolle: (4|7|0) und (7|4|0)] | + | [Zur Kontrolle: (4|7|0) und (7|4|0)] |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:ABI_2004_V_1c_Lös.jpg|750px]] | + | [[Bild:ABI_2004_V_1c_Lös.jpg|750px]][[Bild:ABI_2004_V_1c2_Lös.jpg|750px]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Bild:ABI_2004_V_1c2_Lös.jpg|750px]] | + | |
}} | }} | ||
Version vom 13. April 2010, 18:37 Uhr
|
|
|
E: x1 + x2 - 4 x3 + 7 = 0 gegeben.
|
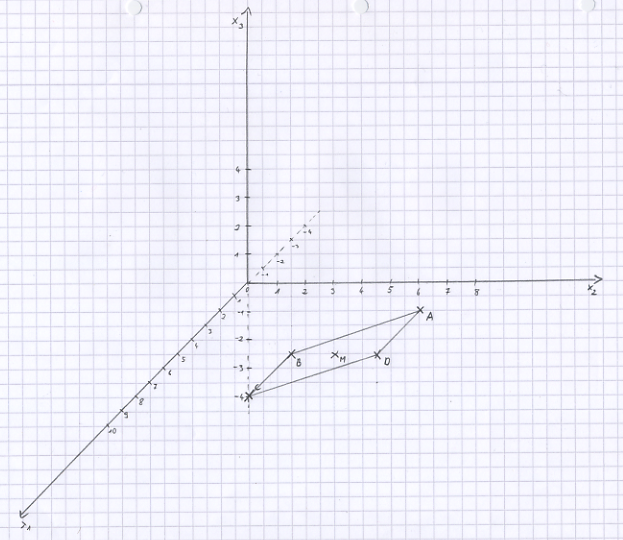
a) Bestimmen Sie die Koordinaten des Punktes D so, dass das Viereck ABCD ein Parallelogramm ist, und berechnen Sie die Koordinaten des Diagonalenschnittpunkts M. Legen Sie ein Koordinatensystem an (Querformat, Ursprung in Seitenmitte) und tragen Sie das Parallelogramm ABCD sowie den Punkt M ein. [Zur Kontrolle: M(4|5|-0,5)]
[Zur Kontrolle: (4|7|0) und (7|4|0)]
|
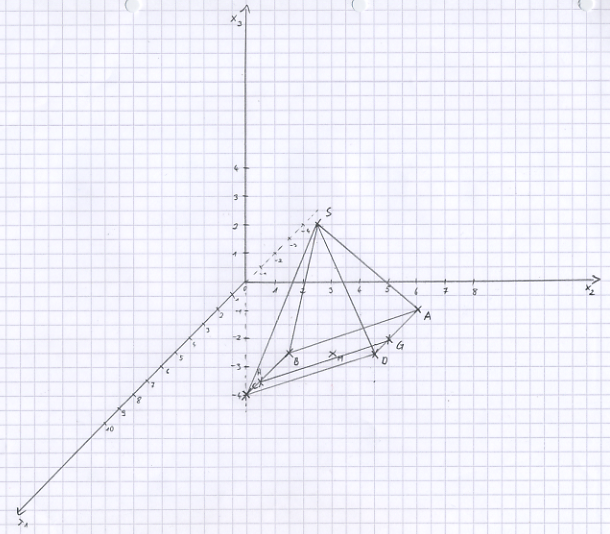
a) S ist der Punkt in E, der vom Diagonalenschnittpunkt M den geringsten Abstand hat. Berechnen Sie die Koordinaten von S und zeichnen Sie die Pyramide ABCDS in Ihre Zeichnung ein. [Zur Kontrolle: S(3|4|3,5)]
|
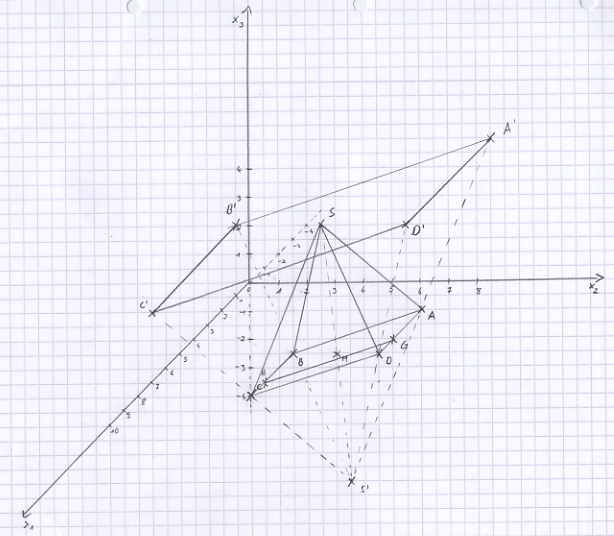
S' sei der Spiegelpunkt von S bezüglich der Ebene, in der das Parallelogramm ABCD liegt. a) Berechnen Sie die Koordinaten von S' und tragen Sie S' in die Zeichnung ein.
b) Berechnen Sie die Koordinaten des Bildpunktes A' von A. Tragen Sie ohne weitere Rechnung das Bildviereck A'B'C'D' in die Zeichnung ein
|