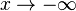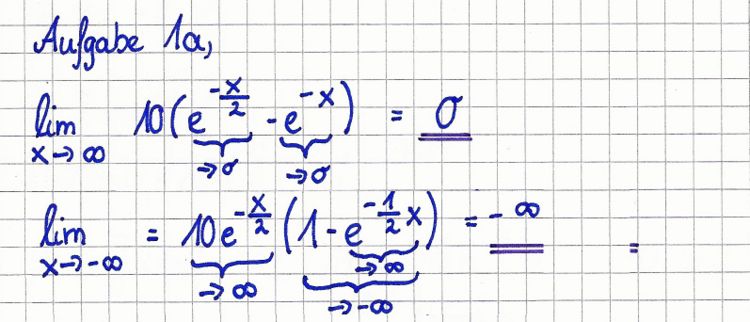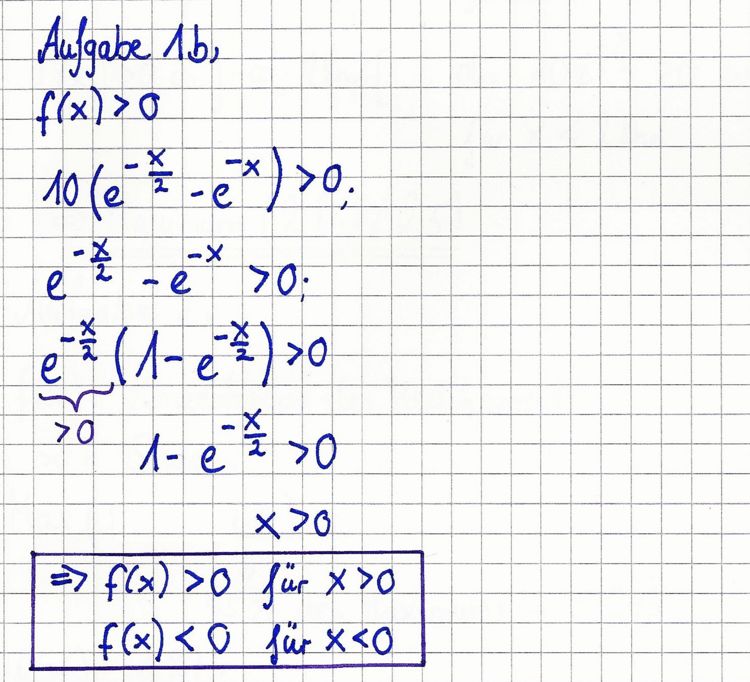2004 I: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(abi_2004) |
(abi_2004) |
||
| Zeile 36: | Zeile 36: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_1_a.jpg|750px]] |
}} | }} | ||
| Zeile 42: | Zeile 42: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_1_b.jpg|750px]] |
}} | }} | ||
| − | c | + | ;c |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_1_c.jpg|700px]] |
}} | }} | ||
| Zeile 55: | Zeile 55: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[ | + | [[Bild:Abi_2004_2_a.jpg|500px]] |
}} | }} | ||
Version vom 9. April 2010, 21:59 Uhr
|
ruth, vroni, julian
|
|
a) das Verhalten von
Einem Patienten wird zum Zeitpunkt x=0 eine bestimmte Menge eines Medikamentes verabreicht.
Der obige Term f(x) beschreibt die Konzentration dieses Medikaments (Anzahl der Milliliter pro Liter Blut) nach x Stunden.
|
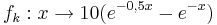 .
Der zugehörige Graph ist nebenstehend skizziert.
.
Der zugehörige Graph ist nebenstehend skizziert.
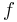 für
für 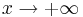 und
und