2004 II: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung | + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2004'''</big></center> |
<center><big>'''Infinitesimalrechnung II'''</big></center> | <center><big>'''Infinitesimalrechnung II'''</big></center> | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID= | + | <center> [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=3b6f5b35e5627e5c952006db5cc4aa9d'''Download der Originalaufgaben: Abitur 2004 LK Mathematik Bayern'''] |
| − | + | ||
| + | Erarbeitet von Johanna Buchner, Isabell Geist und Ann Christin Werner</center> | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 28. März 2010, 15:30 Uhr
|
|
Gegeben ist die Funktion
a) Berechnen Sie die Nullstelle von f und untersuchen Sie das Verhalten von f an den Rändern von Df.
[[Bild:]]
[[Bild:]]
[[Bild:]]
|
Zwei Gänge von 2,0 m und 4,0 m Breite treffen rechtwinklig aufeinander. Es soll die größtmögliche Länge L eines Balkens ermittelt werden, den man in horizontaler Lage aus einem Gang in den anderen tragen kann. Die Dicke des Balkens wird als vernachlässigbar klein angesehen.
[[Bild:]]
[[Bild:]]
|
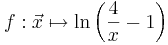 mit dem maximalen Definitionsbereich Df = ]0;4[. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = ]0;4[. Der Graph von f wird mit Gf bezeichnet.
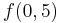 . Zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte).
. Zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte).
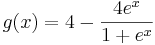 . Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein.
. Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein.
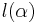 ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° <
ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° <  < 90° die Funktion
< 90° die Funktion  .
.
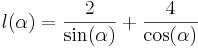 .
.

