2005 I: Unterschied zwischen den Versionen
| Zeile 63: | Zeile 63: | ||
[[Bild: 2006_1_1d.jpg|750px]] | [[Bild: 2006_1_1d.jpg|750px]] | ||
</popup> | </popup> | ||
| − | < | + | <div align="Right"><i>'''5 BE'''</i></div> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <b>e)</b> Bestätigen Sie, dass für k E |R gilt: <math>f_k(x) = w(x) -f_{k}^{'}(x)</math> | ||
| + | Der Grapg G<sub>1</sub> begrenzt im ersten Quadranten mit der x-Achse ein sich ins Unendliche erstreckendes Flächenstück mit endlichen Inhalt. Berechnen Sie diesen Flächeninhalt der obigen Beziehung. | ||
| + | <popup name= "Lösung"> | ||
| + | [[Bild: 2005_1_1d.jpg|750px]] | ||
| + | </popup> | ||
| + | <dic align="Right"><i>'''7 BE'''</i> | ||
</div> | </div> | ||
Version vom 15. März 2010, 17:38 Uhr
|
|
|
Aufgabe 1 Gegeben ist die Schar der in |R definierten Funktionen fk(x)=(x2 + 1 - k)e-x mit k E |R Der Graph von fk wird mit Gkbezeichnet. a) Untersuchen Sie fk auf Nullstellen in Abhängigkeit von k. Bestimmen Sie das Verhalten von fk für x->-8 und x->+8. 4 BE
b) Zeigen Sie, dass sich je zwei verschiedene Graphen Gk nicht schneiden, einander aber beliebig nahe kommen. 4 BE
c) Für welche Werte von k besitzt Gk mindestens eine waagrechte Tangente? Zeigen Sie, dass sie Punkte von Gk mit waagrechter Tangente auf dem Graphen W der Funktion w: x->2xe-x mit x E |R liegen. 7 BE
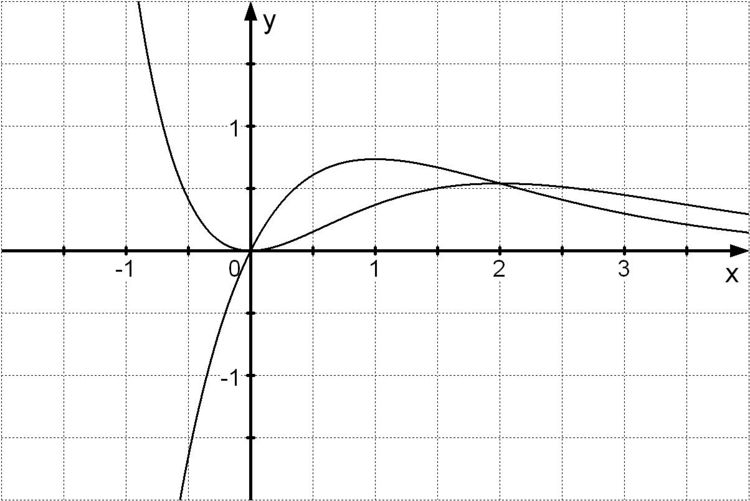
d) Die unten stehende Abbildung zeigt die Graphen G1 und W. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den GRaphen G2 in die Abbildung ein.
5 BE
e) Bestätigen Sie, dass für k E |R gilt: <dic align="Right">7 BE |
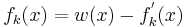Der Grapg G1 begrenzt im ersten Quadranten mit der x-Achse ein sich ins Unendliche erstreckendes Flächenstück mit endlichen Inhalt. Berechnen Sie diesen Flächeninhalt der obigen Beziehung.
