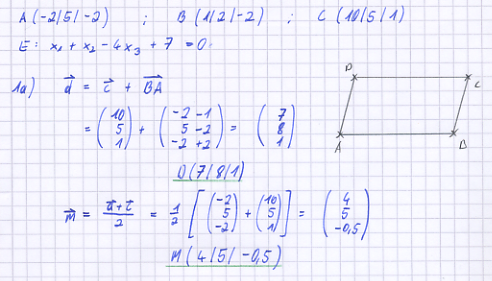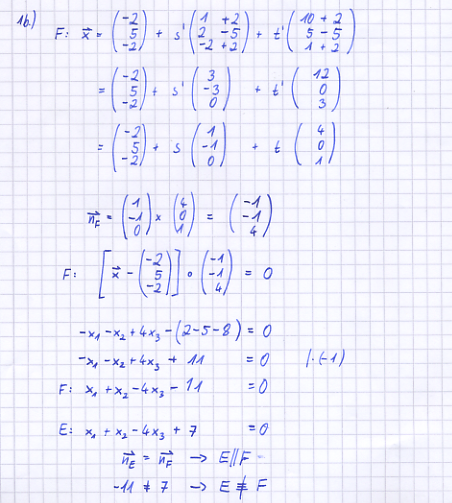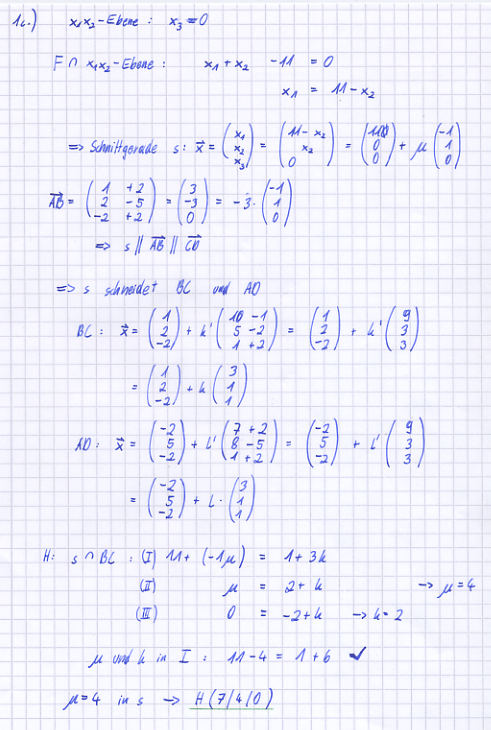2004 V: Unterschied zwischen den Versionen
(seite erstellt) |
K |
||
| Zeile 10: | Zeile 10: | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID= | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=3b6f5b35e5627e5c952006db5cc4aa9d '''Download der Originalaufgaben: Abitur 2004 LK Mathematik Bayern'''] - [[Media:LKM Abi 2004 V lös.doc|Lösungen zum Ausdrucken]]</center> |
| + | |||
| + | <center> Lösungen von Ludwig Deufert, Emanuel Eirich und Simon Markfelder </center> | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 22: | Zeile 24: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | |||
| − | + | In einem kartesischen Koordinatensystem des R³ sind die Punkte A(-2|5|-2), B(1|2|-2), C(10|5|1) sowie die Ebene gegeben. | |
| − | a) | + | </td></tr></table></center> |
| − | + | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
| + | |||
| + | a) Bestimmen Sie die Koordinaten des Punktes D so, dass das Viereck ABCD ein Parallelogramm ist, und berechnen Sie die Koordinaten des Diagonalenschnittpunkts M. | ||
| + | Legen Sie ein Koordinatensystem an (Querformat, Ursprung in Seitenmitte) und tragen Sie das Parallelogramm ABCD sowie den Punkt M ein. | ||
| + | |||
| + | [Zur Kontrolle: M(4|5|-0,5)] | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 35: | Zeile 50: | ||
| − | b) | + | b) Zeigen Sie, dass das Parallelogramm ABCD in einer Parallelebene zur Ebene E liegt, die nicht mit E identisch ist. |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
[[Bild:ABI_2004_V_1b_Lös.jpg|750px]] | [[Bild:ABI_2004_V_1b_Lös.jpg|750px]] | ||
}} | }} | ||
| + | |||
| + | |||
| + | c) Die Parallelogrammfläche schneidet die in der Strecke [GH]. Berechnen Sie die Koordinaten der Punkte der Punkte G und H und tragen Sie die Strecke [GH] in die angelegte Zeichnung ein. | ||
| + | |||
| + | [Zur Kontrolle: (4|7|0) und (7|4|0)] | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2004_V_1c_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | d) In welchem Verhältnis wird die Fläche des Parallelogramms durch die geteilt? Begründen Sie Ihre Antwort. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2004_V_1d_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
Version vom 10. März 2010, 13:57 Uhr
|
|
|
|
a) Bestimmen Sie die Koordinaten des Punktes D so, dass das Viereck ABCD ein Parallelogramm ist, und berechnen Sie die Koordinaten des Diagonalenschnittpunkts M. Legen Sie ein Koordinatensystem an (Querformat, Ursprung in Seitenmitte) und tragen Sie das Parallelogramm ABCD sowie den Punkt M ein. [Zur Kontrolle: M(4|5|-0,5)]
[Zur Kontrolle: (4|7|0) und (7|4|0)]
|
|