2008 VI: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(+Bemerkung 1a) |
|||
| Zeile 32: | Zeile 32: | ||
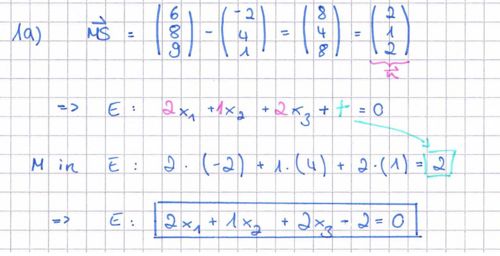
a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.<br />[Zur Kontrolle: E : 2x1 + x2 + 2x3 − 2 = 0] <div align="right">''5 BE''</div> | a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.<br />[Zur Kontrolle: E : 2x1 + x2 + 2x3 − 2 = 0] <div align="right">''5 BE''</div> | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt|1= |
1.Lösung Ebene erstellen | 1.Lösung Ebene erstellen | ||
Version vom 1. März 2010, 08:33 Uhr
|
|
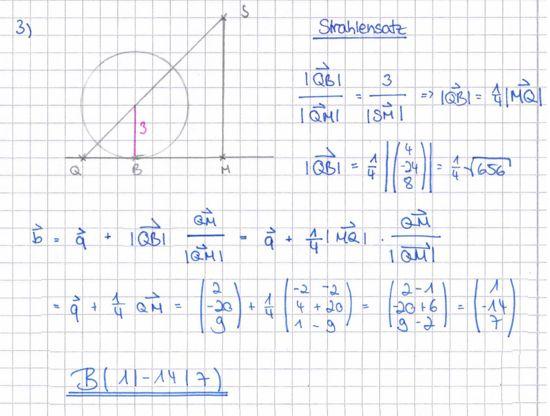
[Teilergebnis: (−12 | 8 | 9) ] 4 BE
3 BE
7 BE
|
8 BE
|
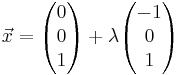 , λ ∈ IR gegeben.
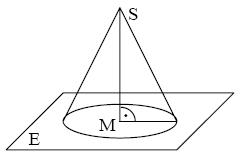
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius
, λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius 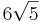 und liegt in der Ebene E.
und liegt in der Ebene E.




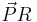 und
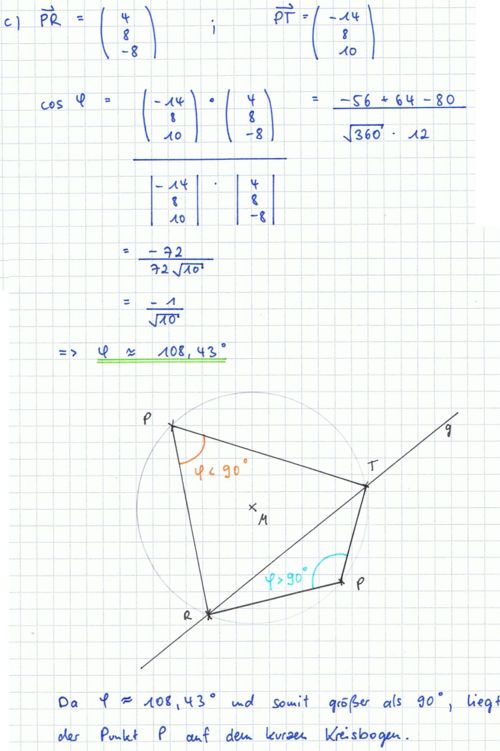
und 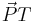 einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort.
einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort.