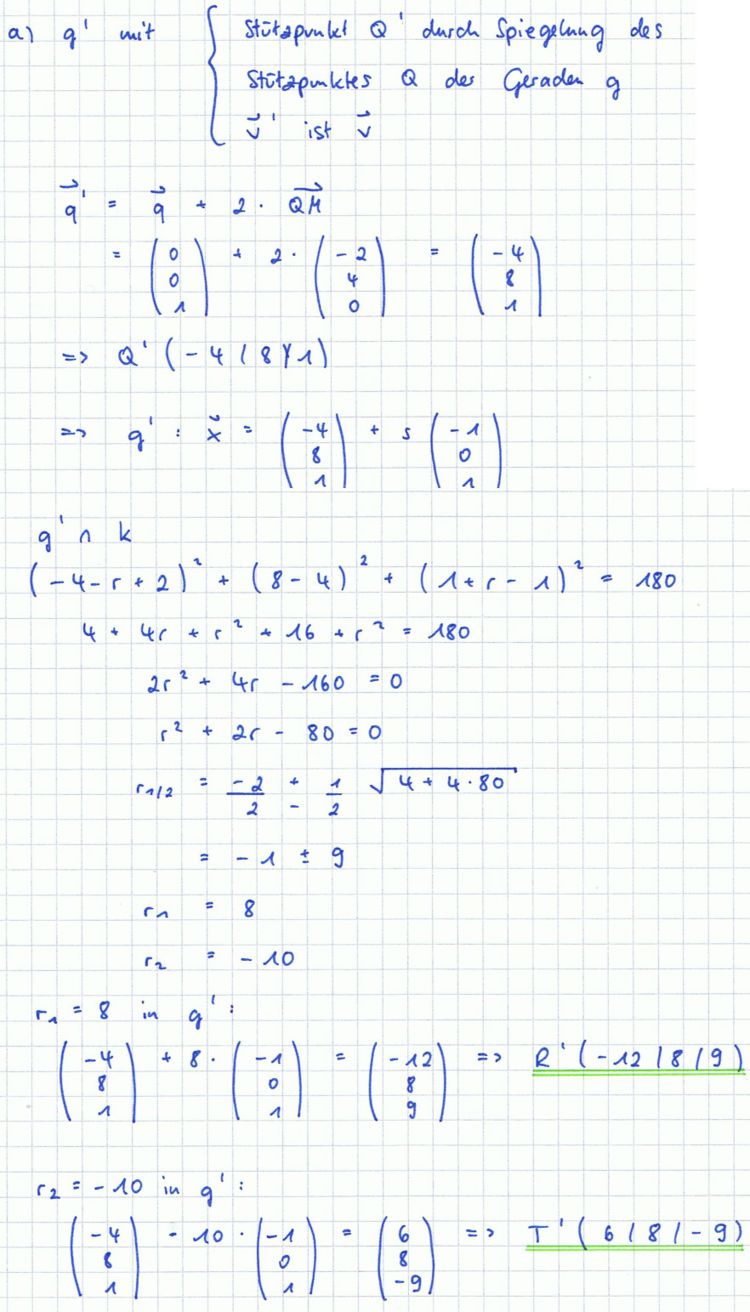2008 VI: Unterschied zwischen den Versionen
(Lösung der Aufgabe 1a) |
(Lösung der Aufgabe 1b) |
||
| Zeile 42: | Zeile 42: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:ABI_2008_VI_1b_Lös.jpg| | + | [[Bild:ABI_2008_VI_1b_Lös.jpg|500px]] |
}} | }} | ||
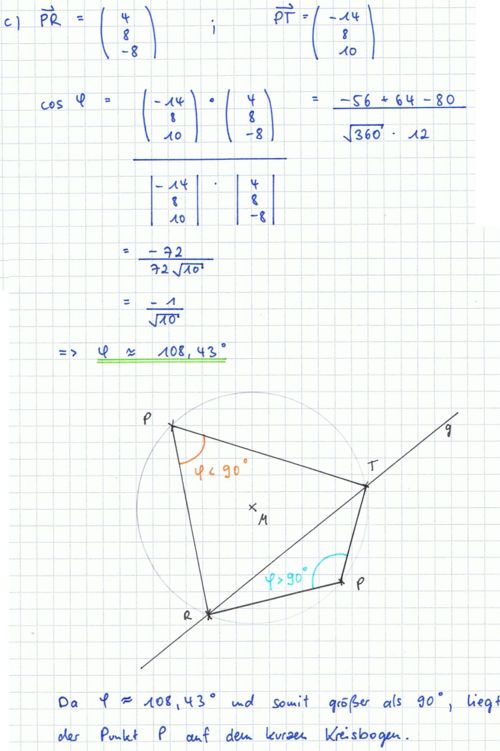
c) Die Gerade g teilt den Grundkreis k in einen kurzen und einen langen Kreisbogen. Berechnen Sie den Winkel ϕ, den die Vektoren <math>\vec PR</math> und <math>\vec PT</math> einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort. | c) Die Gerade g teilt den Grundkreis k in einen kurzen und einen langen Kreisbogen. Berechnen Sie den Winkel ϕ, den die Vektoren <math>\vec PR</math> und <math>\vec PT</math> einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2008_VI_1c_Lös.jpg|500px]] | ||
| + | }} | ||
Version vom 6. Februar 2010, 13:31 Uhr
|
|
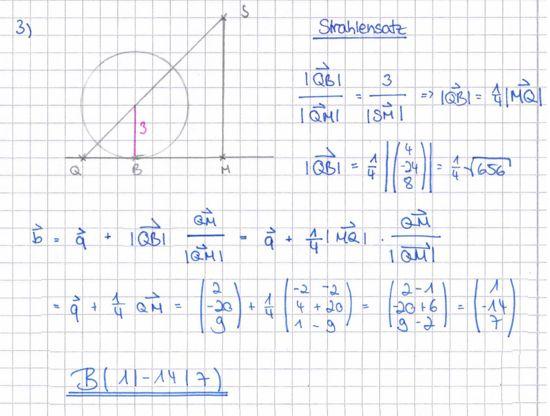
In einem kartesischen Koordinatensystem des IR3 sind die Punkte M(−2 | 4 |1), S(6 | 8 | 9), P(4 | −8 |1) sowie die Gerade g : a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.
|
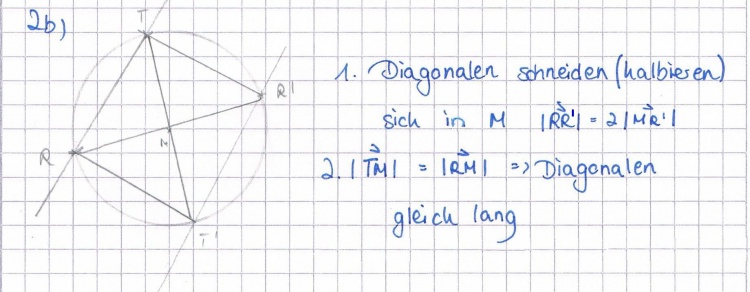
a) Die Spiegelung der Geraden g an M ergibt die Gerade g'. Ermitteln Sie die Koordinaten der Schnittpunkte von g' mit k.
|
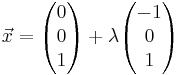 , λ ∈ IR gegeben.
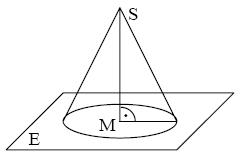
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius
, λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius 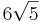 und liegt in der Ebene E.
und liegt in der Ebene E.


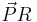 und
und 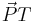 einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort.
einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort.