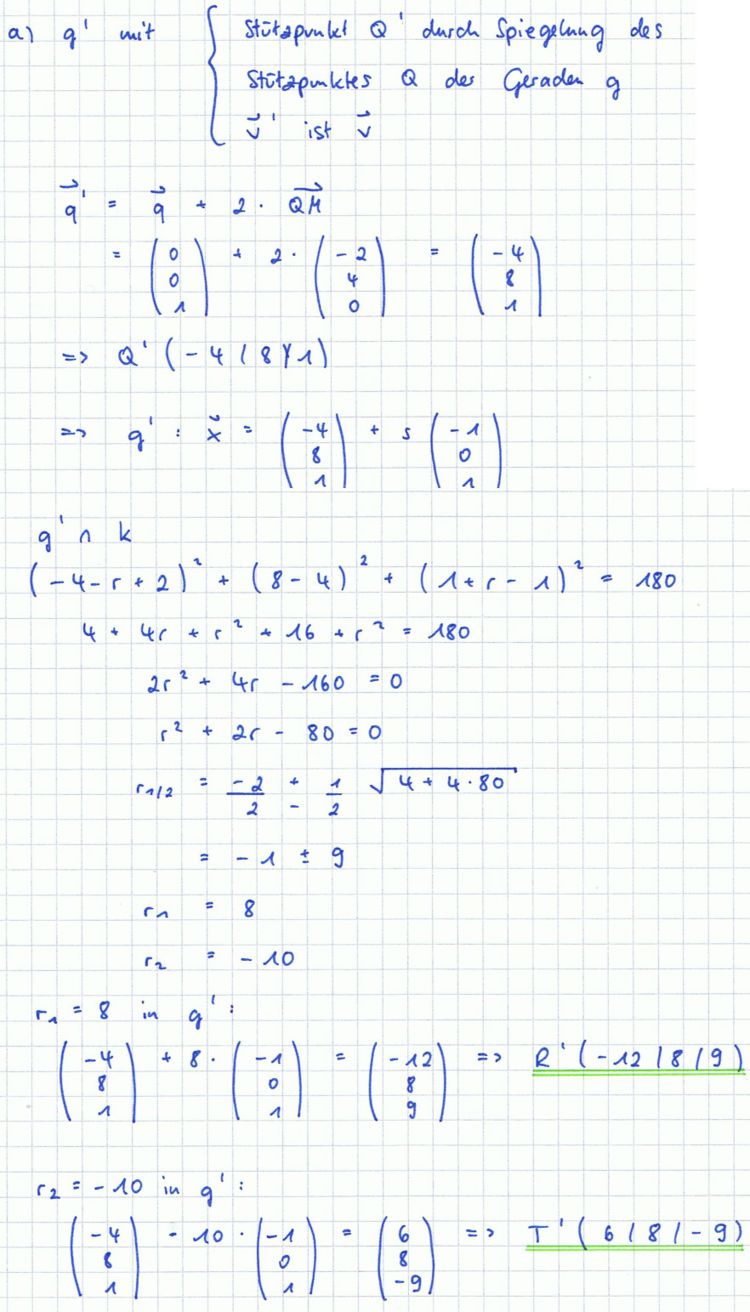2008 VI: Unterschied zwischen den Versionen
(bis Aufgabe 1 a) |
(komplette angabe ohne lösungen) |
||
| Zeile 24: | Zeile 24: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | In einem kartesischen Koordinatensystem des IR<sup>3</sup> sind die Punkte M(−2|4|1), S(6|8|9), P(4|−8|1) sowie die Gerade g : <math>\vec x = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \lambda\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}</math>, λ ∈ IR gegeben. | + | In einem kartesischen Koordinatensystem des IR<sup>3</sup> sind die Punkte M(−2 | 4 |1), S(6 | 8 | 9), P(4 | −8 |1) sowie die Gerade g : <math>\vec x = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \lambda\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}</math>, λ ∈ IR gegeben. |
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius <math>6\sqrt{5}</math> und liegt in der Ebene E. | Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius <math>6\sqrt{5}</math> und liegt in der Ebene E. | ||
| − | + | [[Bild:ABI_2008_VI_Grafik_A1.jpg|center]] | |
a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt. | a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt. | ||
<br />[Zur Kontrolle: E : 2x1 + x2 + 2x3 − 2 = 0] | <br />[Zur Kontrolle: E : 2x1 + x2 + 2x3 − 2 = 0] | ||
| − | [[Bild: | + | :{{Lösung versteckt| |
| + | [[Bild:ABI_2008_VI_1a_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | b) Zeigen Sie, dass die Gerade g in der Ebene E liegt, und bestimmen Sie | ||
| + | die Koordinaten der Schnittpunkte R und T von g und k. (Der Punkt | ||
| + | mit positiver x1-Koordinate wird mit R bezeichnet.) | ||
| + | <br />[Teilergebnis: R(8 | 0 | −7), T(−10 | 0 |11)] | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2008_VI_1b_Lös.jpg|750px]] |
}} | }} | ||
| − | + | c) Die Gerade g teilt den Grundkreis k in einen kurzen und einen langen Kreisbogen. Berechnen Sie den Winkel ϕ, den die Vektoren <math>\vec PR</math> und <math>\vec PT</math> einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort. | |
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | ;Aufgabe 2 | ||
| + | |||
| + | a) Die Spiegelung der Geraden g an M ergibt die Gerade g'. Ermitteln Sie die Koordinaten der Schnittpunkte von g' mit k. | ||
| + | <br />[Teilergebnis: (−12 | 8 | 9) ] | ||
| + | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2008_VI_2a_Lös.jpg|750px]] |
| + | }} | ||
| + | |||
| + | |||
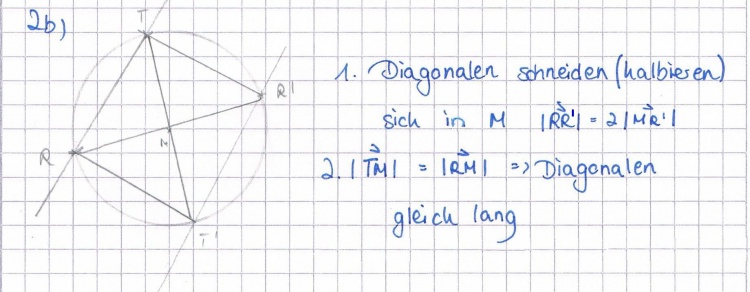
| + | b) Begründen Sie ohne Rechnung, dass die Punkte, in denen die Geraden | ||
| + | g und g' den Kreis k schneiden, ein Rechteck bilden. | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2008_VI_2b_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | c) Das Rechteck aus Teilaufgabe 2b bestimmt zusammen mit dem Punkt | ||
| + | S eine Pyramide. Wie viel Prozent des Kegelvolumens füllt diese | ||
| + | Pyramide aus? | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2008_VI_2c_Lös.jpg|750px]] | ||
}} | }} | ||
| Zeile 52: | Zeile 93: | ||
<div style="padding:1px;background: #EEEEE6;border:0px groove;"> | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| − | |||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
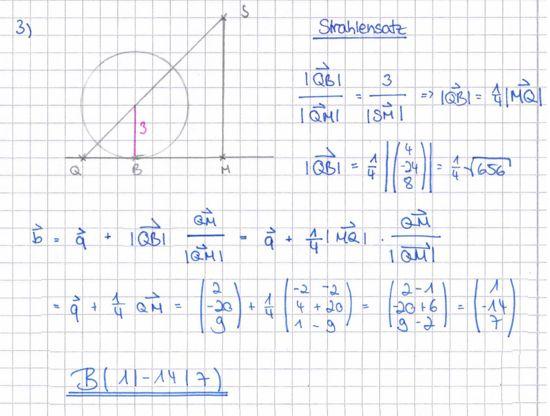
| + | ;Aufgabe 3 | ||
| − | + | Die Spitze S des Kegels wird geradlinig mit dem in der Ebene E liegenden | |
| + | Punkt Q(2 | −20 | 9) verbunden. Auf der Strecke [SQ] bewegt sich | ||
| + | der Mittelpunkt einer Kugel mit Radius 3 auf die Ebene E zu. Berechnen | ||
| + | Sie die Koordinaten des Punktes B, in dem die Kugel die Ebene E | ||
| + | berührt. | ||
| − | + | :{{Lösung versteckt| | |
| − | + | [[Bild:ABI_2008_VI_3_Lös.jpg|750px]] | |
| − | + | }} | |
| + | |||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 5. Februar 2010, 12:27 Uhr
|
|
In einem kartesischen Koordinatensystem des IR3 sind die Punkte M(−2 | 4 |1), S(6 | 8 | 9), P(4 | −8 |1) sowie die Gerade g :  a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.
|
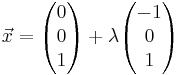, λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius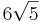 
und liegt in der Ebene E.
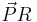und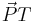 
einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort.
a) Die Spiegelung der Geraden g an M ergibt die Gerade g'. Ermitteln Sie die Koordinaten der Schnittpunkte von g' mit k.
|
Die Spitze S des Kegels wird geradlinig mit dem in der Ebene E liegenden Punkt Q(2 | −20 | 9) verbunden. Auf der Strecke [SQ] bewegt sich der Mittelpunkt einer Kugel mit Radius 3 auf die Ebene E zu. Berechnen Sie die Koordinaten des Punktes B, in dem die Kugel die Ebene E berührt.
|
