Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎1.Verschiebung nach oben/unten)
Zeile 28: Zeile 28:
 
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup> <br />
 
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup> <br />
 
:::<span style="color: green">f(1)=1</span> <br />
 
:::<span style="color: green">f(1)=1</span> <br />
−
Verschiebung um <span style="color: red">3 Einheiten nach oben</span>  <math>\rightarrow</math> g(x)=f(x)+3 <br />
+
Verschiebung um <span style="color: red">3 Einheiten nach oben</span>  → g(x)=f(x)+3 <br />
 
::: g(1)=<span style="color: green">f(1)</span><span style="color: red">+3</span> <br />
 
::: g(1)=<span style="color: green">f(1)</span><span style="color: red">+3</span> <br />
 
::: g(1)=<span style="color: green">1</span><span style="color: red">+3</span> <br />
 
::: g(1)=<span style="color: green">1</span><span style="color: red">+3</span> <br />
Zeile 53: Zeile 53:
  
 
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup>+2x<sup>2</sup>  <br />
 
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup>+2x<sup>2</sup>  <br />
−
:::x=1 <math>\rightarrow</math>  f(1)=3  <br />    <br />                       
+
:::x=1 →  f(1)=3  <br />    <br />                       
 
Verschiebung um <span style="color: red">3 Einheiten nach rechts</span>: <br />
 
Verschiebung um <span style="color: red">3 Einheiten nach rechts</span>: <br />
 
:::g(x)=f(x<span style="color: red">-3</span>) <br />
 
:::g(x)=f(x<span style="color: red">-3</span>) <br />

Version vom 25. Januar 2010, 19:58 Uhr

Inhaltsverzeichnis

Verschieben von Funktionsgraphen

1.Verschiebung nach oben/unten

Problemstellung:


Im nebenstehenden Applet siehst du den Funktionsgraphen f der Funktion f(x)=x3. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt.



Erklärung:
Der Graph f gehört zu dem Funktionsterm f(x)=x3. Der rote Graph g liegt jeweils so viele Einheiten über bzw. unter dem Graphen f, wie der Regler anzeigt.
Man kann also sagen, dass der Graph g   a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x   3 Einheiten größer ist, als der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings um a Einheiten nach oben (in positiver y-Richtung) bzw. nach unten (in negativer y-Richtung) verschoben.

Für den Funktionsterm g(x) gilt somit: g(x)=f(x)+a.

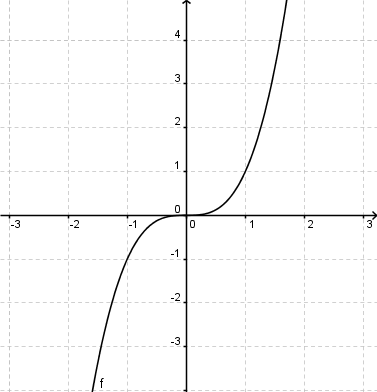
Beispiel: f(x)=x3
f(1)=1

Verschiebung um 3 Einheiten nach oben → g(x)=f(x)+3

g(1)=f(1)+3
g(1)=1+3
g(1)=4



Merke:

Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x)+a entsteht der Graph g durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung.

Für ein positives a erfolgt die Verschiebung in positiver y-Richtung (nach oben), für ein negatives a in negativer y-Richtung (nach unten).




2.Verschiebung nach rechts/links

Problemstellung:
Im untenstehenden Applet siehst du den Graphen f mit x→x3+2x2 und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst.
Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauszufinden.




Erklärung:
Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben
nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings um b Einheiten nach rechts bzw. links verschoben. Somit entspricht
der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.
Das bedeutet für den funktionellen Zusammenhang: g(x)=f(x-3).

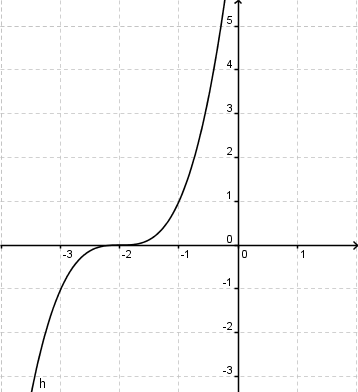
Beispiel: f(x)=x3+2x2
x=1 → f(1)=3

Verschiebung um 3 Einheiten nach rechts:

g(x)=f(x-3)
g(x)=(x-3)3+2(x-3)2
g(4)=(4-3)3+2(4-3)2
g(4)=1+2=3=f(1)


Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von g(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.


Merke:
Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).



3.Beispielaufagben

Aufgabe 1:
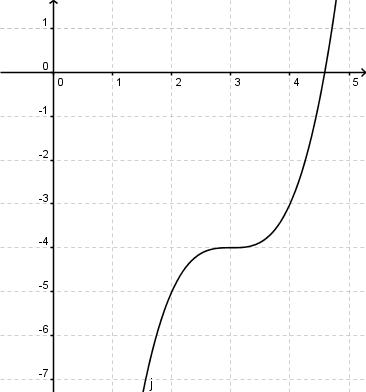
Gegeben ist die Funktion f(x)=x3+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.



Aufgabe 2:
Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x3 hervorgegangen sind.

Ausgangsfunktion:
Aufgabe 1.2 Verschiebungen 1.png

a) Aufgabe 1.2 Verschiebungen 2.png

b) Aufgabe 1.2 Verschiebungen 3.png

c) Aufgabe 1.2 Verschiebungen 4.png




Aufgabe 3:

Kreuze an, was stimmt. Es können mehrere Antwortmöglichkeiten richtig sein.

1. In welche Richtung ist der Graph f(x)=3x4+3x2-2x+4 ist gegenüber dem Graphen g(x)=3x4+3x2-2x verschoben?

nach oben
nach unten
nach links
in positiver y-Richtung
nach rechts

2. Um wie viele Einheiten ist der Graph g(x)=2x3+x2+4 gegenüber dem Graphen f(x)=2x3+x2-2 nach oben verschoben?

4
gar nicht
6
2

3. Wie lautet der Funktionsterm der Funktion, die ausgehend von der Funktion f(x)=x3+2x um 1 Einheit nach unten und 2 Einheiten nach links verschoben ist?

g(x)=x3+2x-1
g(x)=x3+6x2+14x+11
g(x)=x3+2x-3
g(x)=(x+2)3+2(x+2)-1
g(x)=(x-2)3+2(x-2)-1

4. In welche Richtung ist die Funktion g(x)=(x+3)2+2 gegenüber der Funktion f(x)=x2+2 verschoben?

nach links
nach rechts
in positiver y-Richtung
in positiver x-Richtung
in negativer x-Richtung
in negativer y-Richtung
nach oben
nach unten

Punkte: 0 / 0

Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen


Zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=Facharbeit_Florian_Wilk/Verschieben_von_Funktionsgraphen&oldid=28042“