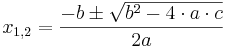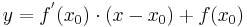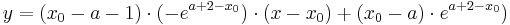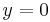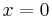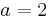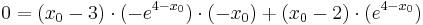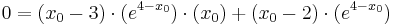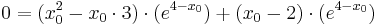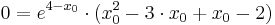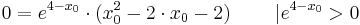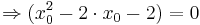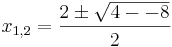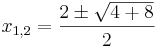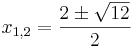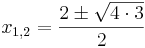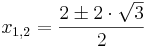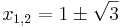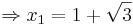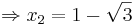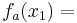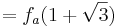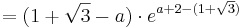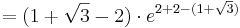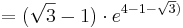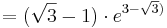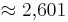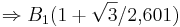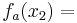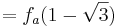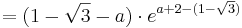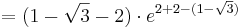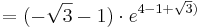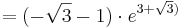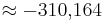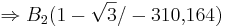Lösung von Teilaufgabe c) 2.: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: == Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f<sub>2</sub> durch den Ursprung verläuft == === Verwendung der Tangentialgleichung === ...)
 
(→‎Verwendung der Tangentialgleichung)
Zeile 45: Zeile 45:
  
 
:      <math>f_a(x_1)=\;</math><br />  
 
:      <math>f_a(x_1)=\;</math><br />  
−
: <math>= f_a(1 + \sqrt{3})\;</math>  
+
::: <math>= f_a(1 + \sqrt{3})\;</math>  
−
: <math>= ( 1 + \sqrt{3} - a )\cdot e^{a + 2 - ( 1 + \sqrt{3})}</math><br />
+
::: <math>= ( 1 + \sqrt{3} - a )\cdot e^{a + 2 - ( 1 + \sqrt{3})}</math><br />
−
:                      <math> = ( 1 + \sqrt{3} - 2 )\cdot e^{2 + 2 - ( 1 + \sqrt{3})}</math><br />
+
:::                      <math> = ( 1 + \sqrt{3} - 2 )\cdot e^{2 + 2 - ( 1 + \sqrt{3})}</math><br />
−
:                      <math> = ( \sqrt{3} - 1 )\cdot e^{4 - 1 - \sqrt{3})}</math><br />
+
:::                      <math> = ( \sqrt{3} - 1 )\cdot e^{4 - 1 - \sqrt{3})}</math><br />
−
:                      <math> = ( \sqrt{3} - 1 )\cdot e^{3 - \sqrt{3})}</math><br />
+
:::                      <math> = ( \sqrt{3} - 1 )\cdot e^{3 - \sqrt{3})}</math><br />
−
:                      <math>\approx 2{,}601</math><br />
+
:::                      <math>\approx 2{,}601</math><br />
  
  
Zeile 58: Zeile 58:
  
 
:      <math>f_a(x_2) =\;</math><br />  
 
:      <math>f_a(x_2) =\;</math><br />  
−
:      <math>= f_a(1 - \sqrt{3})\;</math>  
+
:::      <math>= f_a(1 - \sqrt{3})\;</math>  
−
:                      <math> = ( 1 - \sqrt{3} - a )\cdot e^{a + 2 - ( 1 - \sqrt{3})}</math><br />
+
:::                      <math> = ( 1 - \sqrt{3} - a )\cdot e^{a + 2 - ( 1 - \sqrt{3})}</math><br />
−
:                      <math> = ( 1 - \sqrt{3} - 2 )\cdot e^{2 + 2 - ( 1 - \sqrt{3})}</math><br />
+
:::                      <math> = ( 1 - \sqrt{3} - 2 )\cdot e^{2 + 2 - ( 1 - \sqrt{3})}</math><br />
−
:                      <math> = ( -\sqrt{3} - 1 )\cdot e^{4 - 1 + \sqrt{3})}</math><br />
+
:::                      <math> = ( -\sqrt{3} - 1 )\cdot e^{4 - 1 + \sqrt{3})}</math><br />
−
:                      <math> = ( -\sqrt{3} - 1 )\cdot e^{3 + \sqrt{3})}</math><br />
+
:::                      <math> = ( -\sqrt{3} - 1 )\cdot e^{3 + \sqrt{3})}</math><br />
−
:                     <math>\approx -310{,}164</math><br />
+
:::                  <math>\approx -310{,}164</math><br />
  
  

Version vom 24. Januar 2010, 21:14 Uhr

Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f2 durch den Ursprung verläuft

Verwendung der Tangentialgleichung

y = f^{'}( x_0)\cdot ( x - x_0 ) + f ( x_0 )
y = ( x_0 - a - 1 )\cdot ( -e^{a + 2 - x_0})\cdot ( x - x_0 ) + ( x_0 - a )\cdot e^{a + 2 - x_0})


mit:\;

y = 0\;
x = 0\;
a = 2\;


0 = ( x_0 - 3 )\cdot ( -e^{4 - x_0} )\cdot ( -x_0 ) + ( x_0 - 2 )\cdot ( e^{4 - x_0} )
0 = ( x_0 - 3 )\cdot ( e^{4 - x_0} )\cdot ( x_0 ) + ( x_0 - 2 )\cdot ( e^{4 - x_0} )
0 = ( x_0^{2} - x_0\cdot 3 )\cdot ( e^{4 - x_0} ) + ( x_0 - 2 )\cdot ( e^{4 - x_0} )
0 = e^{4 - x_0}\cdot ( x_0^{2} - 3\cdot x_0 + x_0 - 2 )
0 = e^{4 - x_0}\cdot ( x_0^{2} - 2\cdot x_0 - 2 )\;\;\;\;\;\;\;\;|e^{4 - x_0}>0
\Rightarrow ( x_0^{2} - 2\cdot x_0 - 2 ) = 0

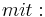
Lösen quadratischer Gleichungen mit Hilfe der Mitternachtsformel x_{1,2} = \frac{-b\pm\sqrt{b^{2}-4\cdot a\cdot c}}{2a}

x_{1,2} = \frac{2\pm\sqrt{4--8}}{2}
x_{1,2} = \frac{2\pm\sqrt{4+8}}{2}
x_{1,2} = \frac{2\pm\sqrt{12}}{2}
x_{1,2} = \frac{2\pm\sqrt{4\cdot 3}}{2}
x_{1,2} = \frac{2\pm2\cdot\sqrt{3}}{2}
x_{1,2} = {1\pm\sqrt{3}}


\Rightarrow x_{1} = {1 + \sqrt{3}}
\Rightarrow x_{2} = {1 - \sqrt{3}}


f_a(x_1)=\;
= f_a(1 + \sqrt{3})\;
= ( 1 + \sqrt{3} - a )\cdot e^{a + 2 - ( 1 + \sqrt{3})}
= ( 1 + \sqrt{3} - 2 )\cdot e^{2 + 2 - ( 1 + \sqrt{3})}
= ( \sqrt{3} - 1 )\cdot e^{4 - 1 - \sqrt{3})}
= ( \sqrt{3} - 1 )\cdot e^{3 - \sqrt{3})}
\approx 2{,}601


\Rightarrow B_1(1 + \sqrt{3} / 2{,}601)


f_a(x_2) =\;
= f_a(1 - \sqrt{3})\;
= ( 1 - \sqrt{3} - a )\cdot e^{a + 2 - ( 1 - \sqrt{3})}
= ( 1 - \sqrt{3} - 2 )\cdot e^{2 + 2 - ( 1 - \sqrt{3})}
= ( -\sqrt{3} - 1 )\cdot e^{4 - 1 + \sqrt{3})}
= ( -\sqrt{3} - 1 )\cdot e^{3 + \sqrt{3})}
\approx -310{,}164


\Rightarrow B_2(1 - \sqrt{3} / -310{,}164)




Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_c/Lösung_von_Teilaufgabe_c)_2.&oldid=27969“