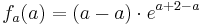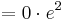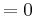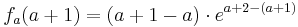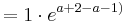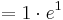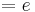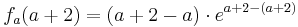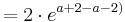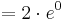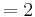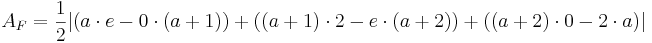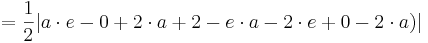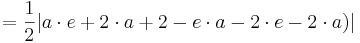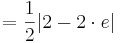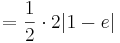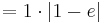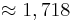Lösung von Teilaufgabe d: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 48: Zeile 48:
 
Mit den nun drei bestimmten Punkten '''R<sub>a</sub>''', '''H<sub>a</sub>''' und '''W<sub>a</sub>''' lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.
 
Mit den nun drei bestimmten Punkten '''R<sub>a</sub>''', '''H<sub>a</sub>''' und '''W<sub>a</sub>''' lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.
  
−
<ggb_applet width="728" height="359"  version="3.2" ggbBase64="UEsDBBQACAAIADajNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VhNb+M2ED3v/gpCpxZdx/qwHAews9iklwDZpoC3e+iloKSxzEYiXZFK5Pz6DoeSrMReI24XRXowKA5Hw5k3b4aU5x+bsmAPUGmh5MILznyPgUxVJmS+8GqzGs28j5fv5zmoHJKKs5WqSm4WXnQWelZei8v37+Z6rR4ZL0jlq4DHhWeqGjymNxXwTK8BjBOveKFRzutGFIJX27vkT0iN3i04GzdyU5vOSFpmt0J30zHttymE+Vk8iAwqVqh04U1j9ByfvkJlRMqLhTfxnSTEsKbPF1EU2dW1qsSTksaq74yvUMKYFk+Ab4ZWNh9TnHOo00JkgksbDPmBSow9isysF148DdEkiHxt8YnPnbVUqSpbbrWBkjW/Q6UWXhjEFuetm0VuptEv3DD2aWk4IzPwsARjMCua8QZ0h01eiawHz05u9JUqdqKNEtJc842pK8po1IqWZmvt41aV9feTzAtoZRhEuob0PlHN0mEQOdNftht6hfxJ8mtVqIpV+EIco0I7Jm4kHetor+WTjk8arQ1rtF8PLkLSoDFxI2kVQjrX2sCDLurA77YRmlmBRRGJ2GFT8AQwsR6rpTC33QQJcN9GGjj9X+oywQIYUqA3GXwnk/PxC+7M76GSUDiGSExsrWrNHiwTXerIjwxSUeLULbSAcJus39ABJ80gr6Dz25WPg4tW/SELX4jn484J64NGX1ODbQDjMTYWW6YGS8Q+ZdxYia2BAkrAAjHEBlmXUIm0R4b/YdvCuzluUrdbhR2FqUkoKvgXeO6Ax+VvMAZbw2bN8eksaHnBt1j8wyDJ2meVtRu3erqgLlEK7G8jKrWSN1ha9oknWhW1gWWKEMpblXJDfdB519Z14FNNNrZpUHF2VboSDexK7XAz2bHXrJEmErSmEjPDYuISs0zQY5vYuBixdwI4Bna6bIMxUxn3FEFeuXzYzDTYbbVt5B2un7CZN2jvB0zLB4Y+/9gZoybgsfFeQtuF3sC/TRw1hT51/itTN2SttsiHLfCE+5M7qEjFdTPbhunFaA+Uo3SFfbKeB7NwZn+T+MKfxAeo2+b7v+AuMcxJBs2pOzyfLxynwtWACuwnhvh9YHAqHa7eCh2ilg776TqNHHswXT+HKbQwhafXzfVbAWrSA3Vi3aSqLLnMmOQlRverKra5khSVsHczxn1qLzwgavHQxuwCqk23jiddgReJwKmlTo3jEC28xG3YbnMATrdhB1hv6tU99dvgD87XIfpBHBH+cfCPq9Y/3n005HbWO5J+j2gOU+lIMMe5dLdaaTCWOqMwJuqMgtnruDY6UI3b9pviyR64k2gaT+3vIpj5Fyecj/CXdDra3bJEiff/VJiecYU9Fm+kwTsX0B1m/yp1D7CxN9g7+aXiUtvvmCP982je+JvOm72un5I2/2XWgmdpG03OZudREOIvmkXT3ur/MG/J287bzOH+yrR1N6JRuEuU/5ZzMx5+Y9A3dfufwuXfUEsHCAzavNtTBAAAhRAAAFBLAQIUABQACAAIADajNzwM2rzbUwQAAIUQAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAjQQAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
+
<ggb_applet width="773" height="412"  version="3.2" ggbBase64="UEsDBBQACAAIAM2jNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vjvbts2EP+8PgWhTxtW26JsuTZgp9g6DA2QLcPctcC+DLR0trhIpEdSiZzn2ZvsxXY8Srbj/EGMDUUaIJB4PB7v7ve7I+XZ26Yq2TUYK7WaR7wfRwxUpnOp1vOodqveJHp79mq2Br2GpRFspU0l3Dwa9pPIy2t59uqrmS30DRMlqXyUcDOPnKkhYnZjQOS2AHBBvBKlRbmoG1lKYbaXyz8hc3Y/EWycq03tOiNZlV9I2w0HtN+mlO4HeS1zMKzU2Twap+g5vn0E42Qmynk0ioMkwbDGdydRNPSzhTbyVivn1ffGVyhhzMpbwJWJl80GFOcM6qyUuRTKB0N+oBJjNzJ3BboQv0GTINcF+jricbCWaW3yxdY6qFjzOxg9jxKe+jxvw2gYRhb9wg3TmKYOR2QGrhfgHKJimWjAdrlZG5nvkucH5/Z7Xe5FGy2Veyc2rjaE6LAVLdzW28etjPf3O7UuoZUlmPECsqulbhYhB8Ng+sN2Q0vIn+X6nS61YQYXpCkqtM9leJKOd3SnFZNOTBqtDW90N8+nCWnQcxmepFVKFVxrA+dd1F2GRSMt8wKfRSRil5tSLAGBjVitpLvoBkiAqzZSHvR/rqslFsAhBXYm+f9kcjY44s7sCoyCMjBEIbC1ri279kwM0JEfOWSywmGYaBMiPFi/oQNBmsPaQOd3KJ+QLpq9w8Ij8WzQOeF9sOhr5rANYDzOx+LL1GGJ+LdcOC/xNVBCBVggjtig6gqMzHaZEZHfDbeo2414v/WaWoSmcj/K5j7tOP0IX7AxbAqBb33eskJssfQPQyRrP+m827jdtqQeUUnsbj0qtEo0WFj+TSytLmsHiwwTqC50Jhx1weBdW9U8popsfMug0uxqdCUb2Bfaw61kz11XIEkUWEsF5g5LSSjEmBKPTWITYsTOCRD41+myDcZMRbwjCLIqoOFxabDXWt/Gu7z++ofAZt6gxa/Fa4Y+f9MZoxYQscE9ONuJAwP/FTpqCjvw4meCd8ha63PvaeRTT5m/DQcVqYRu5tswLRzeS8uTdIVjuib9N3ySTPz/KJ3Go/QB8raIfw72EseC5KA5dYfn3YmnyfD+gAzsW4b5e83gVEK8fzmESFpC3AfsNHrcS9Snu4lKfKKS02vn08tJ1XCXqhNrJ9NVJVTOlKgwvl90uV1rRVFJfz9jIm6bjOAtwUQSIg9h1a7T+rH852+8VCipClG6sOCmW2DoZTiPirByNmg3fiDFwYUuhUdmn91xTwWFp0OCJeUnFvTlamXBeRB6PIDQSx4H7fG+ZWHtRzs3b1p2fe5on+bgQbQjTtGOn8fQ3gNVvCWi3v1LiL/I5zGfDid8OuJpPElHJ5y18JcKOjbc12SFXxKZdDvGlv6IPVcOb29At6H7l7IrgI2/C1+qD0Yo67+InujET+JoXjiO/urvScsnzwMyPsaRd0AScr1RP5lO0phPUh6PJ9PueP0SoSu+DOiS9HnIJe3dttedEvjyogtrcPjJQp/o7U8UZ/8CUEsHCNfgQxduBAAA1BAAAFBLAQIUABQACAAIAM2jNzzX4EMXbgQAANQQAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAqAQAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
  
 
== Flächeninhalt des Dreiecks ==
 
== Flächeninhalt des Dreiecks ==

Version vom 23. Januar 2010, 20:31 Uhr

Inhaltsverzeichnis

Kongruenz der Dreiecke

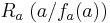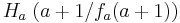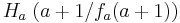Die Dreiecke werden durch die Punkte \; R_a\;( a / f_a (a)), H_a\; ( a + 1 / f_a ( a + 1 )) und H_a\; ( a + 1 / f_a ( a + 1 )) festgelegt.


1.Punkt : 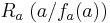\; R_a\;( a / f_a (a))

f_a (a) = ( a - a )\cdot e^{ a + 2 - a }
= 0\cdot e^{ 2 }
= 0\;

Der Punkt Ra liegt für alle a bei Ra ( a / 0 )


2.Punkt : 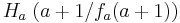H_a\; ( a + 1 / f_a ( a + 1 ))

f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }
= 1 \cdot e^{ a + 2 - a-1) }
= 1 \cdot e^{1}
= e\;

Der Punkt Ha liegt für alle a bei Ha ( a + 1 / e )


3.Punkt : 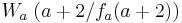W_a\;( a + 2 / f_a ( a + 2 ))

f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }
= 2 \cdot e^{ a + 2 - a-2) }
= 2 \cdot e^{0}
= 2 \;

Der Punkt Wa liegt für alle a bei Wa ( a + 2 / 2 )


Mit den nun drei bestimmten Punkten Ra, Ha und Wa lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.

Flächeninhalt des Dreiecks

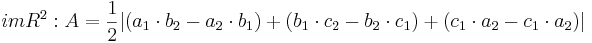
im R^{2}: A = \frac{1}{2} | ( a_1\cdot b_2 - a_2\cdot b_1) + ( b_1\cdot c_2 - b_2\cdot c_1 ) + ( c_1\cdot a_2 - c_1\cdot a_2 ) | 

siehe Formelsammlung Seit 81

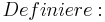
Definiere: \;
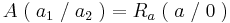
A\; (\;a_1 \;/\; a_2 \;) = R_a \;(\; a \;/\; 0\; )
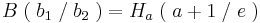
B\; (\;b_1 \;/\; b_2 \;) = H_a \;( \;a + 1\; /\; e \;)
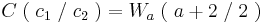
C\; (\;c_1 \;/\; c_2 \;) = W_a \;(\; a + 2 \;/ \;2 \;)


A_F = \frac{1}{2} | ( a\cdot e - 0\cdot (a+1)) + ( (a+1)\cdot 2 - e\cdot (a+2) ) + ( (a+2)\cdot 0 - 2\cdot a ) |
= \frac{1}{2} | a\cdot e - 0 + 2\cdot a + 2- e\cdot a -2\cdot e + 0 - 2\cdot a ) |
= \frac{1}{2} | a\cdot e + 2\cdot a + 2- e\cdot a -2\cdot e - 2\cdot a ) |
= \frac{1}{2} | 2 -2\cdot e |
= \frac{1}{2}\cdot2 | 1 - e |
= 1\cdot | 1 - e |
= | 1 - e |\;
\approx 1,718

Der Flächeninhalt beträgt, unabhängig von a, 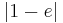| 1 - e |\;.

Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_d/Lösung_von_Teilaufgabe_d&oldid=27704“