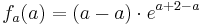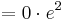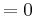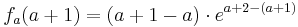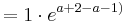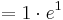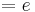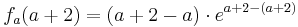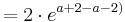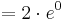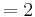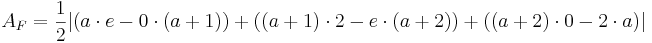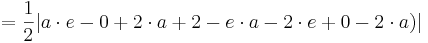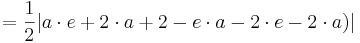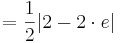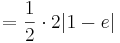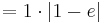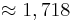Lösung von Teilaufgabe d: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Kongruenz der Dreiecke)
Zeile 1: Zeile 1:
 
== Kongruenz der Dreiecke ==
 
== Kongruenz der Dreiecke ==
  
−
Die Dreiecke werden durch die Punkte '''R<sub>a</sub>''' ( a / f <sub>a</sub> (a) ), '''H<sub>a</sub>''' ( a + 1 / f <sub>a</sub> ( a + 1 )) und '''W<sub>a</sub>''' ( a + 2 / f<sub>a</sub> ( a + 2 )) festgelegt.
+
Die Dreiecke werden durch die Punkte <math>\; R_a\;( a / f_a (a))</math>, <math>H_a\; ( a + 1 / f_a ( a + 1 ))</math> und <math>H_a\; ( a + 1 / f_a ( a + 1 ))</math> festgelegt.
  
−
<u>1.Punkt : '''R<sub>a</sub>''' ( a / f <sub>a</sub> (a))</u>
 
  
−
        <math>f_a (a) = ( a - a )\cdot e^{ a + 2 - a }</math><br />
+
=== 1.Punkt :  <math>\; R_a\;( a / f_a (a))</math> ===
−
          <math> = 0\cdot e^{ 2 }
+
 
 +
 
 +
:        <math>f_a (a) = ( a - a )\cdot e^{ a + 2 - a }</math><br />
 +
 
 +
:::          <math> = 0\cdot e^{ 2 }</math><br />
 
   
 
   
−
                = 0 </math><br />
+
:::          <math> = 0\;</math>  
 
      
 
      
−
Der Punkt '''R<sub>a</sub>''' liegt für alle a bei '''R<sub>a</sub>''' ( a / 0 )
+
Der Punkt '''R<sub>a</sub>''' liegt für alle a bei '''R<sub>a</sub>''' ( a / 0 )
  
  
−
<u>2.Punkt : '''H<sub>a</sub>''' ( a + 1 / f <sub>a</sub> ( a + 1 ))</u>
 
  
−
    <math>f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }</math><br />
+
=== 2.Punkt : <math>H_a\; ( a + 1 / f_a ( a + 1 ))</math> ===
−
          <math> = 1 \cdot e^{ a + 2 - a-1) }</math><br />
+
 
−
          <math> = 1 \cdot  e^{1}
+
 
−
          = e </math><br />
+
:    <math>f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }</math><br />
 +
 
 +
::::          <math> = 1 \cdot e^{ a + 2 - a-1) }</math><br />
 +
 
 +
::::          <math> = 1 \cdot  e^{1}</math><br />
 +
 
 +
::::          <math> = e\; </math><br />
 
   
 
   
−
Der Punkt '''H<sub>a</sub>''' liegt für alle a bei '''H<sub>a</sub>''' ( a + 1 / e )
+
Der Punkt '''H<sub>a</sub>''' liegt für alle a bei '''H<sub>a</sub>''' ( a + 1 / e )
  
−
<u>3.Punkt : '''W<sub>a</sub>''' ( a + 2 / f<sub>a</sub> ( a + 2 ))</u>
 
  
−
    <math>f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }</math><br />
+
 
−
        <math> = 2 \cdot e^{ a + 2 - a-2) }</math><br />
+
=== 3.Punkt : <math>W_a\;( a + 2 / f_a ( a + 2 ))</math> ===
−
        <math> = 2 \cdot  e^{0}
+
 
−
          = 2 </math><br />
+
 
 +
:    <math>f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }</math><br />
 +
 
 +
::::        <math> = 2 \cdot e^{ a + 2 - a-2) }</math><br />
 +
 
 +
::::        <math> = 2 \cdot  e^{0}</math><br />
 +
 
 +
::::          <math>= 2 \;</math><br />
 
   
 
   
−
Der Punkt '''W<sub>a</sub>''' liegt für alle a bei '''W<sub>a</sub>''' ( a + 2 / 2 )
+
Der Punkt '''W<sub>a</sub>''' liegt für alle a bei '''W<sub>a</sub>''' ( a + 2 / 2 )
 +
 
  
 
Mit den nun drei bestimmten Punkten '''R<sub>a</sub>''', '''H<sub>a</sub>''' und '''W<sub>a</sub>''' lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.
 
Mit den nun drei bestimmten Punkten '''R<sub>a</sub>''', '''H<sub>a</sub>''' und '''W<sub>a</sub>''' lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.
Zeile 37: Zeile 52:
 
== Flächeninhalt des Dreiecks ==
 
== Flächeninhalt des Dreiecks ==
  
−
<math>im R^{2}: A = \frac{1}{2}  | ( a_1\cdot  b_2 - a_2\cdot b_1) + (  b_1\cdot c_2 - b_2\cdot c_1 ) + ( c_1\cdot a_2 - c_1\cdot a_2 ) |</math>
+
<math>im R^{2}: A = \frac{1}{2}  | ( a_1\cdot  b_2 - a_2\cdot b_1) + (  b_1\cdot c_2 - b_2\cdot c_1 ) + ( c_1\cdot a_2 - c_1\cdot a_2 ) |</math>
 
   
 
   
 
  siehe Formelsammlung Seit 81
 
  siehe Formelsammlung Seit 81
  
−
Definiere:  
+
<math>Definiere: \;</math><br />
−
A (a<sub>1</sub> / a<sub>2</sub> ) =  '''R<sub>a</sub>''' ( a / 0 )
+
<math> A\; (\;a_1 \;/\; a_2 \;) =  R_a \;(\; a \;/\; 0\; )</math><br />
−
B (b<sub>1</sub> / b<sub>2</sub> ) =  '''H<sub>a</sub>''' ( a + 1 / e )
+
<math> B\; (\;b_1 \;/\; b_2 \;) =  H_a \;( \;a + 1\; /\; e \;)</math><br />
−
C (c<sub>1</sub> / c<sub>2</sub> ) =  '''W<sub>a</sub>''' ( a + 2 / 2 )
+
<math> C\; (\;c_1 \;/\; c_2 \;) =  W_a \;(\; a + 2 \;/ \;2 \;)</math><br />
  
−
<math> A_F = \frac{1}{2}  | ( a\cdot  e - 0\cdot (a+1)) + ( (a+1)\cdot 2 - e\cdot (a+2) ) + ( (a+2)\cdot 0 - 2\cdot a ) |</math>
+
 
−
    <math>  = \frac{1}{2}  |  a\cdot  e - 0 +  2\cdot a + 2- e\cdot a -2\cdot e  +  0 - 2\cdot a ) |</math>
+
: <math> A_F = \frac{1}{2}  | ( a\cdot  e - 0\cdot (a+1)) + ( (a+1)\cdot 2 - e\cdot (a+2) ) + ( (a+2)\cdot 0 - 2\cdot a ) |</math><br />
−
    <math>  = \frac{1}{2}  |  a\cdot  e  +  2\cdot a + 2- e\cdot a -2\cdot e  - 2\cdot a ) |</math>
+
::    <math>  = \frac{1}{2}  |  a\cdot  e - 0 +  2\cdot a + 2- e\cdot a -2\cdot e  +  0 - 2\cdot a ) |</math><br />
−
    <math>  = \frac{1}{2}  |  2 -2\cdot e  |</math>
+
::    <math>  = \frac{1}{2}  |  a\cdot  e  +  2\cdot a + 2- e\cdot a -2\cdot e  - 2\cdot a ) |</math><br />
−
    <math>  = \frac{1}{2}\cdot2 |  1 - e |</math>
+
::    <math>  = \frac{1}{2}  |  2 -2\cdot e  |</math><br />
−
    <math>  = 1\cdot |  1 - e |
+
::    <math>  = \frac{1}{2}\cdot2 |  1 - e |</math><br />
 +
::    <math>  = 1\cdot |  1 - e |</math><br />
 
   
 
   
−
            = |  1 - e  |</math>
+
::      <math>      = |  1 - e  |\;</math><br />
−
    <math>\approx  1,718</math>
+
 
 +
::    <math>\approx  1,718</math><br />
 
   
 
   
−
Der Flächeninhalt beträgt, unabhängig von a, | 1 - e |.
+
Der Flächeninhalt beträgt, '''unabhängig''' von '''a''', <math>| 1 - e |\;</math>.

Version vom 23. Januar 2010, 20:14 Uhr

Inhaltsverzeichnis

Kongruenz der Dreiecke

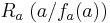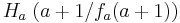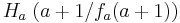Die Dreiecke werden durch die Punkte \; R_a\;( a / f_a (a)), H_a\; ( a + 1 / f_a ( a + 1 )) und H_a\; ( a + 1 / f_a ( a + 1 )) festgelegt.


1.Punkt : 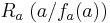\; R_a\;( a / f_a (a))

f_a (a) = ( a - a )\cdot e^{ a + 2 - a }
= 0\cdot e^{ 2 }
= 0\;

Der Punkt Ra liegt für alle a bei Ra ( a / 0 )


2.Punkt : 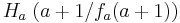H_a\; ( a + 1 / f_a ( a + 1 ))

f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }
= 1 \cdot e^{ a + 2 - a-1) }
= 1 \cdot e^{1}
= e\;

Der Punkt Ha liegt für alle a bei Ha ( a + 1 / e )


3.Punkt : 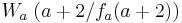W_a\;( a + 2 / f_a ( a + 2 ))

f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }
= 2 \cdot e^{ a + 2 - a-2) }
= 2 \cdot e^{0}
= 2 \;

Der Punkt Wa liegt für alle a bei Wa ( a + 2 / 2 )


Mit den nun drei bestimmten Punkten Ra, Ha und Wa lässt sich sagen, dass die Dreiecke kongruent sein müssen. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben lassen. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschieben kann und somit immer kongruent ist.

BILD (GEOGEBRA) EINFÜGEN

Flächeninhalt des Dreiecks

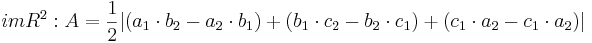
im R^{2}: A = \frac{1}{2} | ( a_1\cdot b_2 - a_2\cdot b_1) + ( b_1\cdot c_2 - b_2\cdot c_1 ) + ( c_1\cdot a_2 - c_1\cdot a_2 ) | 

siehe Formelsammlung Seit 81

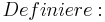
Definiere: \;
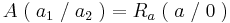
A\; (\;a_1 \;/\; a_2 \;) = R_a \;(\; a \;/\; 0\; )
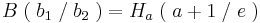
B\; (\;b_1 \;/\; b_2 \;) = H_a \;( \;a + 1\; /\; e \;)
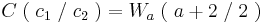
C\; (\;c_1 \;/\; c_2 \;) = W_a \;(\; a + 2 \;/ \;2 \;)


A_F = \frac{1}{2} | ( a\cdot e - 0\cdot (a+1)) + ( (a+1)\cdot 2 - e\cdot (a+2) ) + ( (a+2)\cdot 0 - 2\cdot a ) |
= \frac{1}{2} | a\cdot e - 0 + 2\cdot a + 2- e\cdot a -2\cdot e + 0 - 2\cdot a ) |
= \frac{1}{2} | a\cdot e + 2\cdot a + 2- e\cdot a -2\cdot e - 2\cdot a ) |
= \frac{1}{2} | 2 -2\cdot e |
= \frac{1}{2}\cdot2 | 1 - e |
= 1\cdot | 1 - e |
= | 1 - e |\;
\approx 1,718

Der Flächeninhalt beträgt, unabhängig von a, 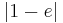| 1 - e |\;.

Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_d/Lösung_von_Teilaufgabe_d&oldid=27702“