Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen
(→2.Verschiebung nach rechts/links) |
(→3.Beispielaufagben) |
||
| Zeile 87: | Zeile 87: | ||
[[Bild:Aufgabe 1.2 Verschiebungen 1.png|400px]] <br /> <br /> | [[Bild:Aufgabe 1.2 Verschiebungen 1.png|400px]] <br /> <br /> | ||
| − | a) [[Bild:Aufgabe 1.2 Verschiebungen 2.png|400px]] <br /> | + | a) [[Bild:Aufgabe 1.2 Verschiebungen 2.png|400px]] <br /> <br /> |
| − | b) [[Bild:Aufgabe 1.2 Verschiebungen 3.png|400px]] <br /> | + | |
| + | b) [[Bild:Aufgabe 1.2 Verschiebungen 3.png|400px]] <br /> <br /> | ||
| + | |||
c) [[Bild:Aufgabe 1.2 Verschiebungen 4.png|400px]] <br /> <br /> | c) [[Bild:Aufgabe 1.2 Verschiebungen 4.png|400px]] <br /> <br /> | ||
Version vom 23. Januar 2010, 18:10 Uhr
Verschieben von Funktionsgraphen1.Verschiebung nach oben/untenProblemstellung:
Erklärung:
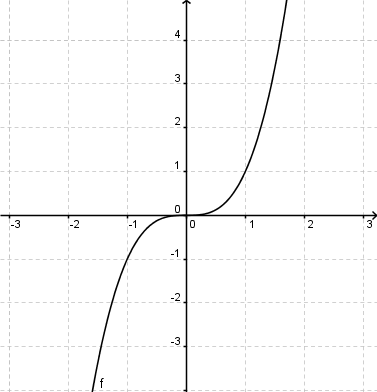
Beispiel: f(x)=x3
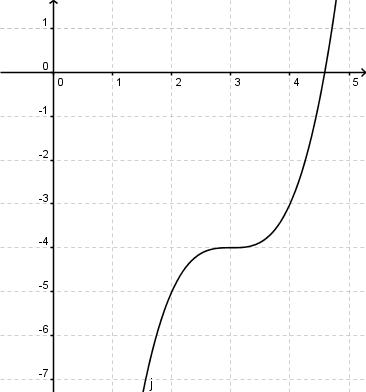
Verschiebung um 3 Einheiten nach oben
Merke: Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x)+a entsteht der Graph g durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung. 2.Verschiebung nach rechts/linksProblemstellung:
Beispiel: f(x)=x3+2x2
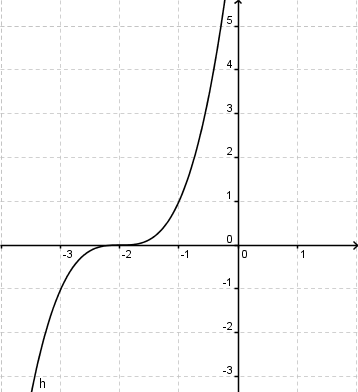
Verschiebung um 3 Einheiten nach rechts:
Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von g(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.
Merke:
Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).
3.Beispielaufagben Aufgabe 1:
Aufgabe 3: |
Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen
 g(x)=f(x)+3
g(x)=f(x)+3