Potenzen: Unterschied zwischen den Versionen
(→Aufgaben: typo) |
(schneeflockenkurve) |
||
| Zeile 117: | Zeile 117: | ||
Von [[Benutzer:Miriam Abert|Miriam Albert]], [[Benutzer:Lang Alicia|Alicia Lang]] und [[Benutzer:Katharina Schneider|Katharina Schneider]]. | Von [[Benutzer:Miriam Abert|Miriam Albert]], [[Benutzer:Lang Alicia|Alicia Lang]] und [[Benutzer:Katharina Schneider|Katharina Schneider]]. | ||
| + | |||
| + | |||
| + | ==Schneeflockenkurve== | ||
| + | [[Bild:Von Koch curve.gif]] | ||
| + | |||
| + | ;Nun mal langsam!!! | ||
| + | #Die Ausgangsfigur ist ein Dreieck mit gleich langen Seiten: | ||
| + | #Der Stern mit 6 Zacken entsteht, indem man auf '''jede Seite''' ein kleines Dreieck aufsetzt. | ||
| + | #Fahre in gleicher Weise fort! | ||
| + | |||
| + | |||
| + | ;Wieviele Seite besitzt die Schneeflockenkurve nach dem | ||
| + | :zweiten Schritt | ||
| + | :dritten Schritt | ||
| + | |||
| + | von[[Benutzer:Patrick Jung|Patrick Jung]] nach einer Idee aus dem Schulbuch, Seite 116. | ||
Version vom 4. April 2008, 20:48 Uhr
zurück: Jahr der Mathematik
Inhaltsverzeichnis |
Was sind Potenzen
Wenn man ein Produkt aus lauter gleichen Faktoren hat, kann man es kurz als Potenz schreiben. Eine Potenz besteht aus der Basis und dem Exponent. Der Exponent gibt an, wie oft die Basis mit sich malgenommen wird.
- Beispiel
- 4 * 4 * 4 * 4 * 4 = 45
- Die Basis ist 4 und der Exponent ist 5.
Die Schachbrettaufgabe
- Auf dem ersten Feld liegt ein 1 Cent Stück, auf dem zweiten doppelt so viel, auf dem dritten wieder das Doppelte.
Berechne oder schätze: (Lösung durch Markieren des grauen Feldes sichtbar machen!)
- Wie viele 1 Cent Stücke liegen auf dem 2-ten, 3-ten, 4-ten,...25-ten Feld? Schau in die Tabelle!
- Wie viele Euro und Cent Stücke liegen auf allen Feldern? 335544,33Euro
- Wenn man die 1 Cent Stücke vom 25. Feld stabelt und jedes 1,7mm dick ist. Wie hoch ist der Stapel? 28km,521m,26cm,7mm
- Wenn ein 1 Cent Stück 2,3g wiegt, wie viele Tonnen, Kilogramm, Gramm wiegen die 1 Cent Stücke auf dem 25. Feld? 38t,587kg,596g
- (ist vergleichbar mit einem Kampfpanzer)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Tricks und Hilfen zu den Lösungen
- Ergebnis auf dem 25.Feld: 224
- Summe aller Münzen auf dem Brett: 225 - 1
von Christian Kempf und Niklas Meißner
Aufgaben
- Schreibe mit Hilfe von Zehnerpotenzen!
610000000 = 61 x 107
40000 = 4 x 104
23000000 = 23 x 106
Jede natürliche Zahl( größer als 1) ist entweder eine Primzahl oder sie lässt sich in ein Produkt aus Primzahlen zerlegen (faktorisieren). Zu jeder Zahl gehört eine bestimmte Primfaktorzerlegung.
- Zerlege 720 in Primfaktoren
720 = 72*10 = 8*9*2*5= 2*2*2*3*3*2*5=
24x32x5
Von Miriam Albert, Alicia Lang und Katharina Schneider.
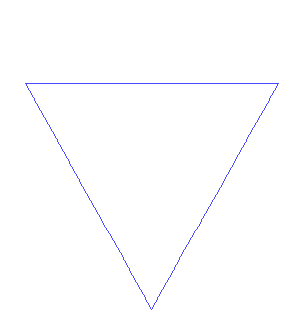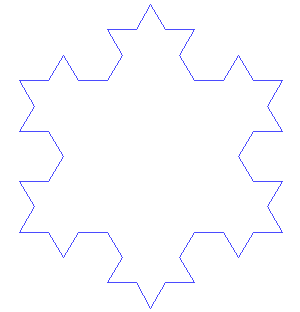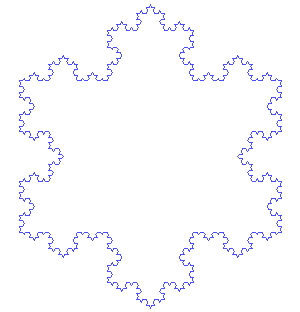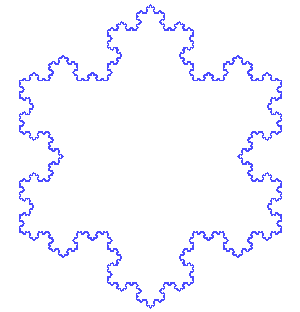
Schneeflockenkurve
- Nun mal langsam!!!
- Die Ausgangsfigur ist ein Dreieck mit gleich langen Seiten:
- Der Stern mit 6 Zacken entsteht, indem man auf jede Seite ein kleines Dreieck aufsetzt.
- Fahre in gleicher Weise fort!
- Wieviele Seite besitzt die Schneeflockenkurve nach dem
- zweiten Schritt
- dritten Schritt
vonPatrick Jung nach einer Idee aus dem Schulbuch, Seite 116.