Grenzwerte im Unendlichen: Unterschied zwischen den Versionen
(→Konvergente Funktionen) |
(→Divergente Funktionen) |
||
| Zeile 99: | Zeile 99: | ||
| − | + | {| | |
| + | ! width="940" | | ||
| + | |- | ||
| + | | valign="top" | | ||
<div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; ">''' <span style="color: red">Merke:</span>''' <br /> | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; ">''' <span style="color: red">Merke:</span>''' <br /> | ||
Nähern sich die Funktionswerte einer Funktion für beliebig groß werdende x-Werte einer Zahl <span style="color: red">a</span> , so ist diese Zahl <span style="color: red">a</span> '''der Grenzwert der Funktion für x gegen plus unendlich'''. <br /> | Nähern sich die Funktionswerte einer Funktion für beliebig groß werdende x-Werte einer Zahl <span style="color: red">a</span> , so ist diese Zahl <span style="color: red">a</span> '''der Grenzwert der Funktion für x gegen plus unendlich'''. <br /> | ||
| Zeile 108: | Zeile 111: | ||
Funktionen, die für x→<math>\infty</math> oder x→ <math>-\infty</math> einen Grenzwert besitzen, nennt man '''konvergent'''. <br /> | Funktionen, die für x→<math>\infty</math> oder x→ <math>-\infty</math> einen Grenzwert besitzen, nennt man '''konvergent'''. <br /> | ||
Funktionen, die für x→<math>\infty</math> und x→<math> -\infty</math> keinen Grenzwert besitzen, nennt man '''divergent'''. </div> <br /> <br /> | Funktionen, die für x→<math>\infty</math> und x→<math> -\infty</math> keinen Grenzwert besitzen, nennt man '''divergent'''. </div> <br /> <br /> | ||
| + | |} | ||
== <span style="color: blue">Beispielaufgaben</span> == | == <span style="color: blue">Beispielaufgaben</span> == | ||
Version vom 18. Januar 2010, 21:47 Uhr
Inhaltsverzeichnis |
Grenzwerte im Unendlichen
|
Eine häufig interessante Eigenschaft von Funktionen ist das Verhalten im Unendlichen. Man interessiert sich also dafür, wie sich ein Funktionsgraph für immer größer bzw. immer kleiner werdende x-Werte verhält. Dieses Verhalten lässt sich oft nicht einfach so aus dem Funktionsterm ablesen. Es gibt aber zwei Möglichkeiten, Hinweise zu erhalten. Zum einen kann das Erstellen einer Wertetabelle weiterhelfen, zum anderen die Umformung des Terms. |
Konvergente Funktionen
|
Aufagbe:
Hinweis: Sonderfall: Betrachtet man den Graphen der Funktion f(x)= |
Divergente Funktionen
Bei divergenten Funktionen, also Funktionen die für x→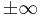 keinen Grenzwert besitzen, unterscheidet man drei verschiedene Möglichkeiten.
keinen Grenzwert besitzen, unterscheidet man drei verschiedene Möglichkeiten.
|
|
|
|
|
|
|
Merke: Nähern sich die Funktionswerte einer Funktion für beliebig groß werdende x-Werte einer Zahl a , so ist diese Zahl a der Grenzwert der Funktion für x gegen plus unendlich.
Dabei ist die Gerade y=a die waagrechte Asymptote des Graphen von f.  und x→ und x→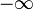 keinen Grenzwert besitzen, nennt man divergent. keinen Grenzwert besitzen, nennt man divergent. |
Beispielaufgaben
Aufgabe 1:
Untersuche die Funktionen auf Grenzwerte.
- a) f(x)=x2
- b) f(x)=2x
- c) f(x)=
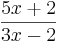
- d) f(x)=
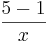
Aufgabe 2:
Ab welchem Funktionswert unterschreitet die Funktion f(x)=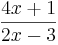 die Abweichung von 0, 1 vom Grenzwert (für x→+∞)?
die Abweichung von 0, 1 vom Grenzwert (für x→+∞)?
Aufgabe 3:
Kreuze die richtigen Antworten an. Es können mehrere Antwortmöglichkeiten richtig sein.
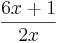 eine Wertetabelle für die x-Werte -20,-15,-10,-8,-5,-3,0,3,5,8,10, 15, 20 und zeichne anhand dieser Werte den Graphen von f. Versuche anhand der Zeichnung einen y-Wert zu erkennen, dem sich der Graph immer weiter annähert. Kontrolliere anschließend dein Ergebnis, indem du den Graphen so umformst, dass man für wachsende x-Werte einen genauen y-Wert ablesen kann.
eine Wertetabelle für die x-Werte -20,-15,-10,-8,-5,-3,0,3,5,8,10, 15, 20 und zeichne anhand dieser Werte den Graphen von f. Versuche anhand der Zeichnung einen y-Wert zu erkennen, dem sich der Graph immer weiter annähert. Kontrolliere anschließend dein Ergebnis, indem du den Graphen so umformst, dass man für wachsende x-Werte einen genauen y-Wert ablesen kann.
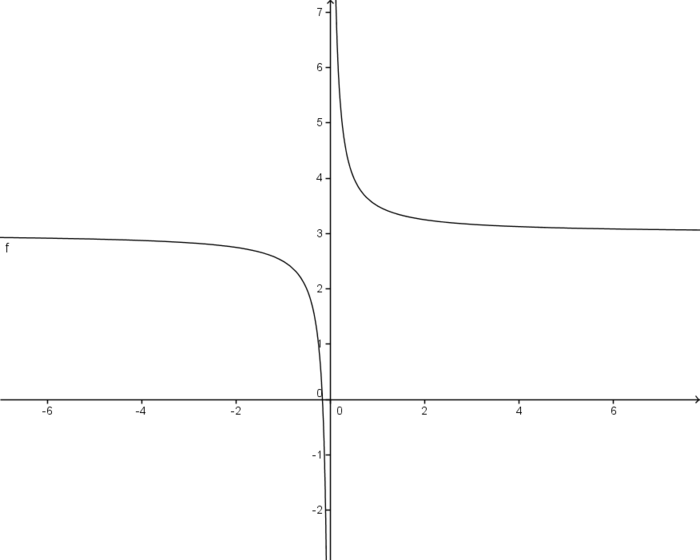
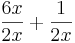 =
=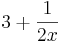
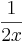 für wachsende x-Werte dem Wert 0 immer näher kommt, kommt die gesamte Funktion dem Wert 3 immer näher. Bei der Zahl 3 spricht man hierbei von dem
für wachsende x-Werte dem Wert 0 immer näher kommt, kommt die gesamte Funktion dem Wert 3 immer näher. Bei der Zahl 3 spricht man hierbei von dem 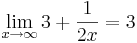
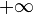 oder
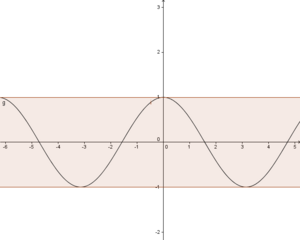
oder 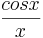 , so fällt auf, dass der Graph um die Asymptote x=0 schwankt, wobei die Schwankung immer kleiner wird.
, so fällt auf, dass der Graph um die Asymptote x=0 schwankt, wobei die Schwankung immer kleiner wird. 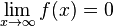
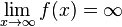 bzw.
bzw. 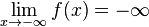
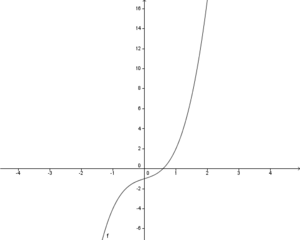
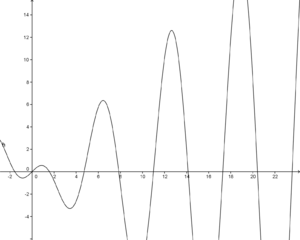
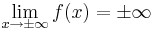 da die Funktionswerte im positiven Bereich für wachsende und im negativen Bereich für immer kleiner werdende x-Werte immer größer werden
da die Funktionswerte im positiven Bereich für wachsende und im negativen Bereich für immer kleiner werdende x-Werte immer größer werden 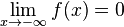 d.h im negativen Bereich nähert sich der Graph für kleiner werdende x-Werte dem Wert 0
d.h im negativen Bereich nähert sich der Graph für kleiner werdende x-Werte dem Wert 0 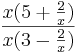 =
=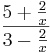
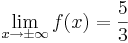 da
da 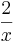 für größer werdende x-Werte gegen 0 geht
für größer werdende x-Werte gegen 0 geht 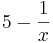
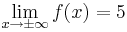 da
da 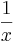 für größer werdende x-Werte gegen 0 geht
für größer werdende x-Werte gegen 0 geht
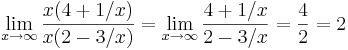
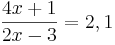 nach x auflösen
nach x auflösen
