Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen
(→2.Verschiebung nach rechts/links) |
(→2.Verschiebung nach rechts/links) |
||
| Zeile 30: | Zeile 30: | ||
'''<span style="color: blue">Problemstellung:</span>''' <br /> | '''<span style="color: blue">Problemstellung:</span>''' <br /> | ||
| − | Im untenstehenden Applett siehst du den Graphen f mit x→x<sup>3</sup>+2x<sup>2</sup> und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst. Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauzufinden. <br /> <br /> | + | Im untenstehenden Applett siehst du den Graphen f mit x→x<sup>3</sup>+2x<sup>2</sup> und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst. <br /> |
| + | Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauzufinden. <br /> <br /> | ||
<ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIANeQMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZRj9M4EH6GX2H5iQVtm6RN25WaRRwnJKTleOgdSDwgOck0MXXsyHa66f76G9tJ2+0d0iLgyfZ4Mv7mm5mvXb/uG0H2oA1XMqPxJKIEZKFKLquMdnZ7vaKvb5+vK1AV5JqRrdINsxmdTRLq7B2/ff5sbWp1T5jwLp843GfU6g4oMa0GVpoawAbzlgmDdtb1XHCmDx/zb1BYc7oIMd7LtrNjkKIp77gZj1P/Xiu4/ZPveQmaCFVkdJEictx9Am15wURG51GwJBlNLi7RNHO3tdL8QUnr3E/Bt2ghxPAHQEISZ1tPfZ5r6ArBS86kS8bjQCdC7nlpa4QwW2BI4FWNWNM4CtEKpXS5ORgLDem/gFbu7ZXj+TCckqU7GcSFD6bLySJaLW7SRZrEy9lNjH7j1Xwyj+PlYr6M0tUqmaXhAdhvwFqslyGsBzOyVmlenu/fmz+UKI9Et4pL+5a1ttO+1LPBtLEH9xYC0i6RN7ISMNgQSlFDsctVvwnkzELovw+t/8TDyau3SihNtKM9RYdhzcPqfRzOo1fkfSLvMcRwQY/38U3iPfyah9V7CS4DtCHveEx6pJ713BBncPRih450CJYDVpySTnJ7Nx6wM3anTJ3/X12T42Sc98YxZPyLQq6nF0213oGWIELrSKxrpzpD9q5FQ+k8jhIK3uAxXAyEMFesfxBAsJZQaRhxh7kKdPnbR+15YV5PRxAOg0GshUV9wHysywXHyBQ1hxwk2aP5XSd37t5UmrU1SDffFmcro++whpgZ+czFjpKSWfzayQb0KAzGaU5gjmByKDx9i+uL/opkpP/6YjaJrsgrkkwi8tKdcXPl0YGABnBGre+7bSc9umMRtvRxd9gayyDxOUfU8NGQvdct5TXoopKnkuP1d3oV1aqtGe4mQzjBDqhH5/T6aB9U+Zh0JrF4nlGUhdYFcO3RApSDBI8gSYsh/Xye1f4JmWFXBY7+w5bsGtC8OOaZe7IQXDdAjCe/mJv4idwMfkZ4UW84/hxdp46MhvUofm7HcqNEZ2FTYGPLO1V4Ekd0gwzHkasHwW/mXlgP7qfAbba8h5MA/r/2P6lrfqZ8jypzMQUZrYYhqMIQ4CyQa5JfUfKEtq9+X9uPQv7Tjf+DrTs9Vx//Mzz8Dbn9F1BLBwj6ycu4WwMAALgIAABQSwECFAAUAAgACADXkDI8+snLuFsDAAC4CAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJUDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> | <ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIANeQMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZRj9M4EH6GX2H5iQVtm6RN25WaRRwnJKTleOgdSDwgOck0MXXsyHa66f76G9tJ2+0d0iLgyfZ4Mv7mm5mvXb/uG0H2oA1XMqPxJKIEZKFKLquMdnZ7vaKvb5+vK1AV5JqRrdINsxmdTRLq7B2/ff5sbWp1T5jwLp843GfU6g4oMa0GVpoawAbzlgmDdtb1XHCmDx/zb1BYc7oIMd7LtrNjkKIp77gZj1P/Xiu4/ZPveQmaCFVkdJEictx9Am15wURG51GwJBlNLi7RNHO3tdL8QUnr3E/Bt2ghxPAHQEISZ1tPfZ5r6ArBS86kS8bjQCdC7nlpa4QwW2BI4FWNWNM4CtEKpXS5ORgLDem/gFbu7ZXj+TCckqU7GcSFD6bLySJaLW7SRZrEy9lNjH7j1Xwyj+PlYr6M0tUqmaXhAdhvwFqslyGsBzOyVmlenu/fmz+UKI9Et4pL+5a1ttO+1LPBtLEH9xYC0i6RN7ISMNgQSlFDsctVvwnkzELovw+t/8TDyau3SihNtKM9RYdhzcPqfRzOo1fkfSLvMcRwQY/38U3iPfyah9V7CS4DtCHveEx6pJ713BBncPRih450CJYDVpySTnJ7Nx6wM3anTJ3/X12T42Sc98YxZPyLQq6nF0213oGWIELrSKxrpzpD9q5FQ+k8jhIK3uAxXAyEMFesfxBAsJZQaRhxh7kKdPnbR+15YV5PRxAOg0GshUV9wHysywXHyBQ1hxwk2aP5XSd37t5UmrU1SDffFmcro++whpgZ+czFjpKSWfzayQb0KAzGaU5gjmByKDx9i+uL/opkpP/6YjaJrsgrkkwi8tKdcXPl0YGABnBGre+7bSc9umMRtvRxd9gayyDxOUfU8NGQvdct5TXoopKnkuP1d3oV1aqtGe4mQzjBDqhH5/T6aB9U+Zh0JrF4nlGUhdYFcO3RApSDBI8gSYsh/Xye1f4JmWFXBY7+w5bsGtC8OOaZe7IQXDdAjCe/mJv4idwMfkZ4UW84/hxdp46MhvUofm7HcqNEZ2FTYGPLO1V4Ekd0gwzHkasHwW/mXlgP7qfAbba8h5MA/r/2P6lrfqZ8jypzMQUZrYYhqMIQ4CyQa5JfUfKEtq9+X9uPQv7Tjf+DrTs9Vx//Mzz8Dbn9F1BLBwj6ycu4WwMAALgIAABQSwECFAAUAAgACADXkDI8+snLuFsDAAC4CAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJUDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> | ||
| − | '''<span style="color: blue">Erklärung:</span>''' Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings um b Einheiten nach rechts bzw. links verschoben. Somit entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.<br /> Das bedeutet für den funktionellen Zusamenhang: g(x)=f(<span style="color: red">x-3</span>). <br /> <br /> | + | '''<span style="color: blue">Erklärung:</span>''' <br /> |
| + | Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben <br /> | ||
| + | nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings <span style="color: blue">um b Einheiten nach rechts bzw. links verschoben</span>. Somit entspricht <br /> | ||
| + | der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.<br /> | ||
| + | Das bedeutet für den funktionellen Zusamenhang: <span style="color: blue">g(x)=f</span>(<span style="color: red">x-3</span><span style="color: blue">)</span>. <br /> <br /> | ||
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup>+2x<sup>2</sup> <br /> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">'''<span style="color: blue">Beispiel:</span>''' f(x)=x<sup>3</sup>+2x<sup>2</sup> <br /> | ||
Version vom 18. Januar 2010, 19:11 Uhr
Inhaltsverzeichnis |
Verschieben von Funktionsgraphen
1.Verschiebung nach oben/unten
Problemstellung:
Im untenstehenden Applett siehst du den Funktionsgraphen f der Funktion f(x)=x3. Den roten Graphen g der Funktion g(x) kannst du durch Verschieben
des Reglers verändern. Versuche herauszufinden, wie sich das Verändern des Parameters auf den Graphen von g auswirkt.
Erklärung:
Der Graph f gehört zu dem Funktionsterm f(x)=x3. Der rote Graph g liegt jeweils so viele Eineiten über bzw unter dem Graphen f, wie der Regler anzeigt.
Man kann also sagen, dass der Graph g a Einheiten über dem Graphen f liegt. Das bedeutet, dass jeder Funktionswert g(x) an der Stelle x 3 Einheiten größer ist, als
der Funktionswert f(x). Folglich nehmen beide Graphen den gleichen Verlauf, allerdings um a Einheiten nach oben (in positiver y-Richtung) bzw.
nach unten (in negativer y-Richtung) verschoben.
- Für den Funktionsterm g(x) gilt somit: g(x)=f(x)+a.
- f(2)=8
- f(2)=8
Verschiebung um 3 Einheiten nach oben  g(x)=f(x)+3
g(x)=f(x)+3
- g(2)=f(2)+3
- g(2)=8+3
- g(2)=11
- g(2)=f(2)+3
Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x)+a entsteht der Graph g durch eine Verschiebung des Graphen f um a Einheiten in y-Richtung.
2.Verschiebung nach rechts/links
Problemstellung:
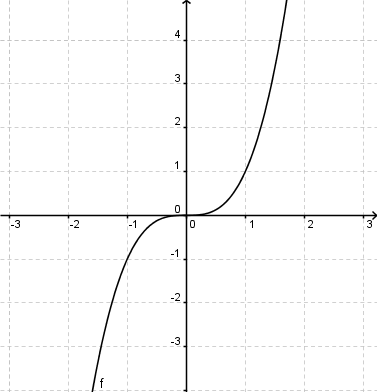
Im untenstehenden Applett siehst du den Graphen f mit x→x3+2x2 und den Graphen g, den du wiederum durch Verändern des Reglers verschieben kannst.
Versuche, einen Zusammenhang zwischen dem Verändern des Reglers und der Verschiebung des Graphen herauzufinden.
Erklärung:
Das Verändern des Reglers führt zu einer Verschiebung des Graphen g nach rechts oder links. Wie schon bei der Verschiebung nach oben
nimmt der Graph dabei den gleichen Verlauf, wie der Graph von f, allerdings um b Einheiten nach rechts bzw. links verschoben. Somit entspricht
der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle x+b.
Das bedeutet für den funktionellen Zusamenhang: g(x)=f(x-3).
- x=1
 f(1)=3
f(1)=3
- x=1
Verschiebung um 3 Einheiten nach rechts:
- g(x)=f(x-3)
- g(x)=(x-3)3+2(x-3)2
- g(4)=(4-3)3+2(4-3)2
- g(4)=1+2=3=f(1)
- g(x)=f(x-3)
Man kann also erkennen, dass der Funktionswert von f(x) an der Stelle 1 gleich dem Funktionswert von g(x) an der Stelle 4, also 3 Einheiten rechts von f(x), ist.
Bei zwei gegebenen Funktionen f und g, für die gilt: g(x)=f(x-b) entsteht der Graph j durch eine Verschiebung um b Einheiten in x-Richtung. Für ein positives b erfolgt die Verschiebung in positiver x-Richtung (nach rechts), für ein negatives b in negativer x-Richtung (nach links).
3.Beispielaufagben
Aufgabe 1:
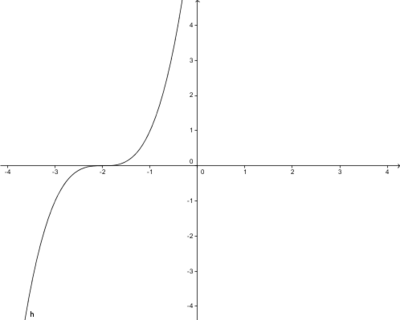
Gegeben ist die Funktion f(x)=x3+5x-5. Bestimme den Funktionsterm h(x) für den Graphen h, der ausgehend vom Graphen f 5 Einheiten nach unten und 2 nach rechts verschoben ist.
Aufgabe 2:
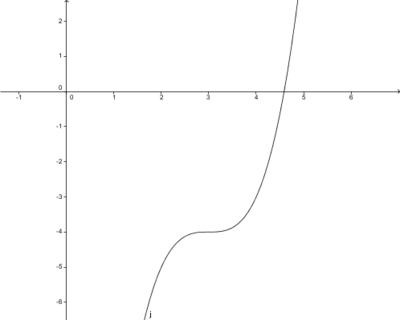
Bestimme die Funktionsterme der Graphen, die durch Verschiebung aus dem Graphen f(x)=x3 hervorgegangen sind.
Aufgabe 3:
Kreuze an, was stimmt. Es können mehrere Antwortmöglichkeiten richtig sein.
Weiter zum Kapitel Strecken und Spiegeln von Funktionsgraphen