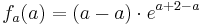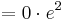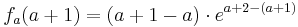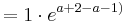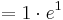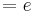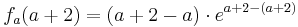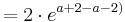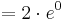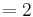Lösung von Teilaufgabe d: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: == Kongruenz der Dreiecke == Die Dreiecke werden durch die Punkte R<sub>a</sub>) |
|||
| Zeile 1: | Zeile 1: | ||
| − | |||
== Kongruenz der Dreiecke == | == Kongruenz der Dreiecke == | ||
| − | Die Dreiecke werden durch die Punkte R<sub>a</sub> | + | Die Dreiecke werden durch die Punkte '''R<sub>a</sub>''' ( a / f <sub>a</sub> (a) ), '''H<sub>a</sub>''' ( a + 1 / f <sub>a</sub> ( a + 1 )) und '''W<sub>a</sub>''' ( a + 2 / f<sub>a</sub> ( a + 2 )) festgelegt. |
| + | |||
| + | <u>1.Punkt : '''R<sub>a</sub>''' ( a / f <sub>a</sub> (a))</u> | ||
| + | |||
| + | <math>f_a (a) = ( a - a )\cdot e^{ a + 2 - a }</math><br /> | ||
| + | <math> = 0\cdot e^{ 2 }</math><br /> | ||
| + | <math> = 0 </math><br /> | ||
| + | |||
| + | Der Punkt '''R<sub>a</sub>''' liegt für alle a bei '''R<sub>a</sub>''' ( a / 0 ) | ||
| + | |||
| + | |||
| + | <u>2.Punkt : '''H<sub>a</sub>''' ( a + 1 / f <sub>a</sub> ( a + 1 ))</u> | ||
| + | |||
| + | <math>f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }</math><br /> | ||
| + | <math> = 1 \cdot e^{ a + 2 - a-1) }</math><br /> | ||
| + | <math> = 1 \cdot e^{1}</math><br /> | ||
| + | <math> = e </math><br /> | ||
| + | |||
| + | Der Punkt '''H<sub>a</sub>''' liegt für alle a bei '''H<sub>a</sub>''' ( a + 1 / e ) | ||
| + | |||
| + | <u>3.Punkt : '''W<sub>a</sub>''' ( a + 2 / f<sub>a</sub> ( a + 2 ))</u> | ||
| + | |||
| + | <math>f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }</math><br /> | ||
| + | <math> = 2 \cdot e^{ a + 2 - a-2) }</math><br /> | ||
| + | <math> = 2 \cdot e^{0}</math><br /> | ||
| + | <math> = 2 </math><br /> | ||
| + | |||
| + | Der Punkt '''W<sub>a</sub>''' liegt für alle a bei '''W<sub>a</sub>''' ( a + 2 / 2 ) | ||
Version vom 5. Januar 2010, 00:56 Uhr
Kongruenz der Dreiecke
Die Dreiecke werden durch die Punkte Ra ( a / f a (a) ), Ha ( a + 1 / f a ( a + 1 )) und Wa ( a + 2 / fa ( a + 2 )) festgelegt.
1.Punkt : Ra ( a / f a (a))
Der Punkt Ra liegt für alle a bei Ra ( a / 0 )
2.Punkt : Ha ( a + 1 / f a ( a + 1 ))
Der Punkt Ha liegt für alle a bei Ha ( a + 1 / e )
3.Punkt : Wa ( a + 2 / fa ( a + 2 ))
Der Punkt Wa liegt für alle a bei Wa ( a + 2 / 2 )