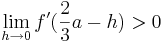Benutzer:Neutert Jan-Peter: Unterschied zwischen den Versionen
(/+3lsg ArtExtremwerte/1versteckt lsg) |
K |
||
| Zeile 94: | Zeile 94: | ||
| − | :'' | + | |
| + | ::<math>\lim_{h\to0} f '(2a + h)> 0</math> und <math>\lim_{h\to0} f '(2a - h)< 0 </math> | ||
| + | |||
| + | ::<math>\lim_{h\to0} f '(\frac{2}{3}a + h)< 0</math> und <math>\lim_{h\to0} f '(\frac{2}{3}a - h)> 0</math> | ||
| + | |||
| + | |||
| + | Daraus ergibt sich nun folgendes Monotonieverhalten. | ||
| + | |||
| + | [[Media:Monotonie.ggb]] | ||
Version vom 1. Januar 2010, 14:18 Uhr
Funktion, Funktion, wie tief ist das Wasser ?
|
So wie im täglichen Leben Statistiken oder Tabellen erstellt werden, können auch in der Mathematik sogenannte Funktionen erstellt werden. Diese sind, ähnlich wie bei einer Tabelle, abhängig von zwei meist unterschiedlichen Größen. Bei den mathematischen Funktionen ist es so, dass einer bestimmten Menge auf der x – Achse, eine bestimmte Menge auf der y - Achse zugeordnet wird. Bei rein mathematischen Überlegungen handelt es sich bei den beiden Mengen um den sogenannten x – Wert beziehungsweise y – Wert. Bei Funktionen mit Einheiten, wie zum Beispiel in der Physik der „Waagrechte Wurf“, wird dem x – Wert die Einheit Länge in Meter gegeben und dem y – Wert Höhe in Meter zugeteilt. Jedoch ist zu beachten, dass bei Funktionen jedem x - Wert nur ein y – Wert zugeordnet werden kann. Es ist also nicht möglich, dass eine Funktion mit dem x – Wert x1 zwei y – Werte y1 und y2 hat. Der Unterschied zwischen einer Funktion und einer Wertetabelle ist lediglich, dass die Funktion eine graphische Abbildung der Wertetabelle darstellt. |
Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorherzusagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar fa mit 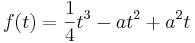 , a > 0
, a > 0
Die Funktion gibt dabei die Durchflussgeschwindigkeit in 106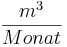 und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage
und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage
(t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet.
• Es soll bestimmt werden, abhängig vom Parameter a, zu welchen Monaten kein Wasser durch den Fluss fließt.
- Was fällt auf, wenn man mit Hilfe des Schiebereglers den Parameter a verändert? Im Applet ist die Funktion als f (x) definiert, nicht als f (t).
- Jede Funktion
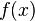 , unabhängig vom Parameter a, schneidet den Ursprung. Das ist die erste Nullstelle, welche der Graph besitzt. Sie ist also unabhänig von a Dies kann man leicht aus der Funktion ablesen, da man eben diese Nullstelle durch einfaches Ausklammern erhält.
, unabhängig vom Parameter a, schneidet den Ursprung. Das ist die erste Nullstelle, welche der Graph besitzt. Sie ist also unabhänig von a Dies kann man leicht aus der Funktion ablesen, da man eben diese Nullstelle durch einfaches Ausklammern erhält.
- Die andere, wie man im Applet sieht eine doppelte Nullstelle, wird mit wachsendem Parameter a immer weiter vom Ursprung entfernt. Sie ist also abhängig von a. Löst man die Quadratische Gleichung erhält man die zweite Nullstelle.
• Es soll, in Abhängigkeit von a, ermittelt werden, zu welchen Zeitpunkten t ein relatives Maximum bzw. Minimum vorliegt. Diese Funktionswerte sollen berechnet werden.
Um die Extremwerte einer Funktion zu errechnen, wird die erste Ableitung benötigt.
|
Die allgemeine Ableitungsregel ist: |
- Bestimme nun die erste Ableitung der Funktion
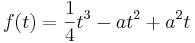
- Bestimme nun die erste Ableitung der Funktion
- Errechne nun die Koordinaten der Extremwerte.
Um die t - Werte der Extremwerte zu erhalten, setzt man die Funktion f '(t) = 0
Da man nun die Gleichung einer quadratischen Gleichung hat, kann man mit Hilfe der "Mitternachtsformel" die beiden Lösungen ausrechnen. Setzt man die errechneten t - Werte in die Funktion ein, erhält man die Koordinaten der Extremwerte E1 und E2.
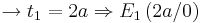
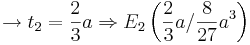
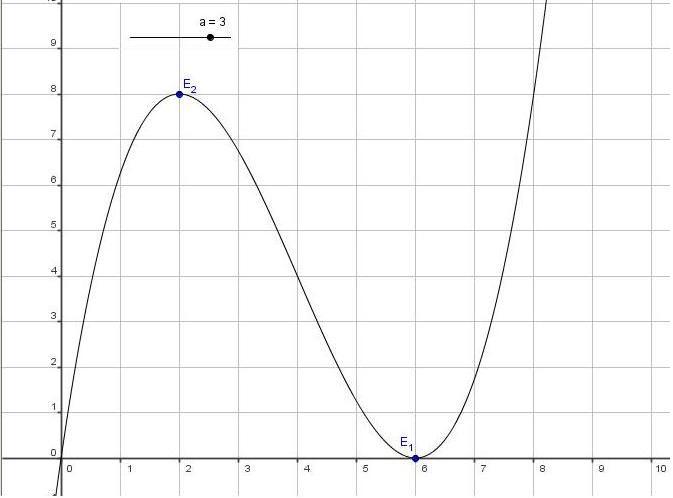
Am Besten sind die Extremwerte für a = 3 zu sehen.
Da sich hier die Koordinaten 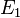 ( 6 / 0 ) und
( 6 / 0 ) und 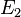 ( 2 / 8 ) ergeben.
( 2 / 8 ) ergeben.
|
Man hat nun die Extremwerte in Abhängigkeit von a ermittelt. Um nun zu prüfen ob es sich bei den Extrema um Maxima oder Minima handelt, kann man hier anhand verschiedener Lösungen vorgehen.
|
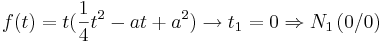
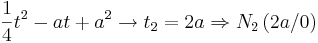
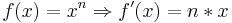 n-1
n-1
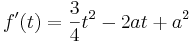
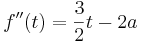
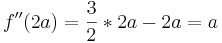
 Rechtskrümmung
Rechtskrümmung 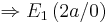 ist Minimum
ist Minimum
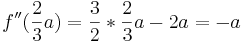
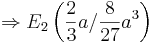 ist Maximum
ist Maximum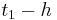 ) und einmal f '(
) und einmal f '(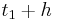 ) ein, um das Verhalten von Gf für t < 2a bzw t > 2a zu bestimmen. Hier ergeben sich je ein positiver und ein negativer Wert, welches die Steigung darstellt. Ist beispielsweise f '(
) ein, um das Verhalten von Gf für t < 2a bzw t > 2a zu bestimmen. Hier ergeben sich je ein positiver und ein negativer Wert, welches die Steigung darstellt. Ist beispielsweise f '(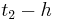 ) und f '(
) und f '(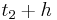 ) ein und erhält somit, ob es sich um ein Maximum oder um ein Minimum handelt.
) ein und erhält somit, ob es sich um ein Maximum oder um ein Minimum handelt.
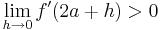 und
und 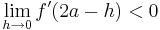
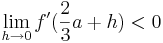 und
und