Geo: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Aufgaben) |
(Hausaufgabe eingefügt) |
||
| Zeile 1: | Zeile 1: | ||
| + | ==Hausaufgabe 17.03.2009== | ||
| + | |||
| + | Die Punkte A(3|-6), B(3|2) und C(-3|2) bilden ein Dreieck. | ||
| + | |||
| + | #Berechnen Sie die Innenwinkel im Dreieck. | ||
| + | #Stellen Sie je eine Gleichung der Winkelhalbierenden w<sub><math>\alpha</math></sub>, w<sub><math>\beta</math></sub> und w<sub><math>\gamma</math></sub> auf. | ||
| + | #Zeigen Sie, dass sich die Winkelhalbierenden in einem Punkt R schneiden. | ||
| + | #Berechnen Sie die (positiven) Abstände des Punktes R von den Dreieckseiten. Welche geometrische Beedeutung hat der Punkt R? | ||
| + | |||
| + | |||
== Hausaufgabe 2.12.2008== | == Hausaufgabe 2.12.2008== | ||
=== Aufgabe 3 (93/3)=== | === Aufgabe 3 (93/3)=== | ||
Version vom 17. März 2009, 17:18 Uhr
Inhaltsverzeichnis |
Hausaufgabe 17.03.2009
Die Punkte A(3|-6), B(3|2) und C(-3|2) bilden ein Dreieck.
- Berechnen Sie die Innenwinkel im Dreieck.
- Stellen Sie je eine Gleichung der Winkelhalbierenden w
 , w
, w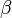 und w
und w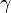 auf.
auf.
- Zeigen Sie, dass sich die Winkelhalbierenden in einem Punkt R schneiden.
- Berechnen Sie die (positiven) Abstände des Punktes R von den Dreieckseiten. Welche geometrische Beedeutung hat der Punkt R?
Hausaufgabe 2.12.2008
Aufgabe 3 (93/3)
- Gib eine Parameterdarstellung der Geraden h(U,V) an mit U(4;-2;1), V(1/2;0;1/3).
- Gib einen Punkt an, der nicht auf h liegt.
- Liegt Q (3;0;2) auf h?
- p sei eine Parallele zu h durch den Punkt P. Gib eine Paramaterdarstellung von h an.
Aufgabe 4 (93/4)
- Bestimme eine Parameterdarstellung der Geraden g(A,B) an mit A(1;3;2), V(5;-2;2)
- Bestimme c so, dass der Punkt C(c;-7;2) auf g liegt.
Hausaufgabe 17.11.2008
Aufgabe 1 (41/3)
Für welche a, b sind die Vektoren 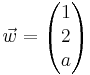 ;
;
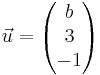 linear abhängig?
linear abhängig?
Aufgabe 2 (42/4)
Zeige, dass die Vektoren 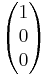 ,
, 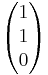 ,
, 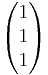 linear unabhängig sind.
linear unabhängig sind.
Warum sind die Vektoren 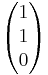 ,
, 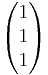 linear unabhängig? (Für den Nachweis gibt es drei Möglichkeiten.)
linear unabhängig? (Für den Nachweis gibt es drei Möglichkeiten.)

