Quiz und Co: Unterschied zwischen den Versionen
| Zeile 431: | Zeile 431: | ||
|} | |} | ||
| + | === Die Krokodilübungen zum Känguruwettbewerb === | ||
| + | |||
| + | Die folgenden Aufgaben können nur eine richtige Antwort enthalten! | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | 1.Wie viel ist 2000-200+20-2 ? (!222) (!1900) (!1902) (1818) (!1919) | ||
| + | |||
| + | |||
| + | 2.Sabine und Sandro haben insgesamt zehn Bonbons. Davon hat Sabine zwei mehr als Sandro. Wie viele Bonbons hat Sandro bekommen? (!8) (!7) (!6) (!5) (4) | ||
| + | |||
| + | |||
| + | 3.Georg lebt zusammen mit seiner Mutter, seinem Vater, einem Bruder, einem Hund, zwei Katzen,zwei Papageien,einem Pferd und vier Goldfischen. Wie viele Beine haben sie alle zusammen? | ||
| + | (!22) (28) (!24) (!32)(!13) | ||
| + | |||
| + | |||
| + | 4.Durch wie viele verschiedene natürliche Zahlen(einschließlich 1 und 36) ist die Zahl 24 ohne Rest teilbar?(!4) (!5) (8) (!9) (!11) | ||
| + | |||
| + | |||
| + | 5. Susanne hat sich eine Zahl ausgedacht und sie dann richtig mit 3 multipliziert. Welche | ||
| + | der folgenden Zahlen war gewiss nicht das Ergebnis? | ||
| + | (!87) (!204) (!444) (103) (!96) | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
Version vom 17. Februar 2009, 08:49 Uhr
Gedichte · Geschichten · Besondere Zahlen · Zahlen im Alltag · Potenzen · Mathe-Rap · Kalender · Geometrie · Symmetrie · Memory, Quiz und Co. · Restekiste
Präsentation des Projekts am Tag des Digitalen Lernens
Ordne der Größe nach
|
Addieren und Multipizieren mit BrüchenZiehe zu jeder Rechnung 2 Ergebnisse
|
Erweitern und Kürzen von Brüchen
Beim Erweitern und Kürzen muss man Zähler und Nenner mit der gleichen Zahl multiplizieren bzw. dividieren. Beim Umwandeln in einen Dezimalbruch bzw. in Prozent muss man den Nenner erst auf eine Stufenzahl bringen.
Ausnahme: Wenn man den Nenner nicht auf eine Stufenzahl bringen kann, dividiert man Zähler durch Nenner um einen Dezimalbruch zu erhalten.
Multiple-Choice-Übung
Kreuze die richtigen Gleichungen an!!!
(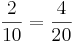 )
(!
)
(!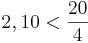 )
(
)
( )
(!
)
(!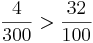 )
(
)
(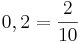 )
(!
)
(!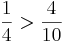 )
(
)
(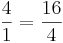 )
(!
)
(!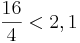 )
(!
)
(!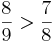 )
(!
)
(!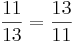 )
)
Kürzen von BrüchenVon Julius-Quirin Karlein und Maximilian Reugels Zuordnung
|
Längen und FlächenWandle die Längen und Flächen um und ziehe die Lösung zur dazugehörigen Länge oder Fläche
|
Multiplizieren von Brüchen
|
SudokuLösung durch Markieren des leeren Feldes sichtbar machen!
|
Memory zu Körpern
|
Multiple-Choice-Übung (Paul + Chrisi)Die folgenden Aufgaben können auch mehrere richtige Antworten enthalten!
|
1. 2. 3. 4. 5. 6. |
Die Krokodilübungen zum Känguruwettbewerb
Die folgenden Aufgaben können nur eine richtige Antwort enthalten!
1.Wie viel ist 2000-200+20-2 ? (!222) (!1900) (!1902) (1818) (!1919)
2.Sabine und Sandro haben insgesamt zehn Bonbons. Davon hat Sabine zwei mehr als Sandro. Wie viele Bonbons hat Sandro bekommen? (!8) (!7) (!6) (!5) (4)
3.Georg lebt zusammen mit seiner Mutter, seinem Vater, einem Bruder, einem Hund, zwei Katzen,zwei Papageien,einem Pferd und vier Goldfischen. Wie viele Beine haben sie alle zusammen?
(!22) (28) (!24) (!32)(!13)
4.Durch wie viele verschiedene natürliche Zahlen(einschließlich 1 und 36) ist die Zahl 24 ohne Rest teilbar?(!4) (!5) (8) (!9) (!11)
5. Susanne hat sich eine Zahl ausgedacht und sie dann richtig mit 3 multipliziert. Welche
der folgenden Zahlen war gewiss nicht das Ergebnis?
(!87) (!204) (!444) (103) (!96)
{|
|width=395px|
|width=5px|<!--Diese Spalte bleibt leer und legt den Abstand zwischen Text und Bild fest-->
|valign="top" |
|}
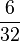 <
< 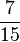 <
<  <
< 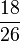
 <
<  <
< 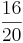 <
< 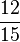
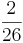 <
< 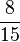 <
<  <
< 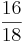
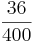 < 12% < 0,78 <
< 12% < 0,78 < 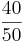
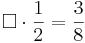


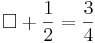


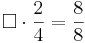


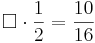
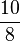

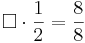
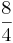


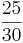
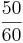
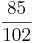
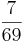
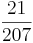
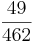
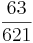
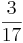
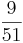
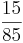
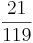
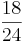
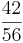
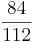


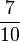
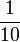
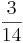
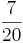

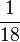
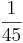
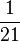
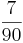
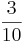
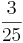
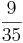
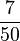

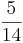

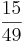

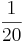
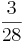
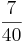



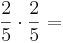 (
(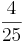 )
(
)
(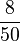 ) (!
) (!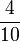 )
)
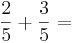 (
( )
(!
)
(!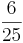 ) (!
) (!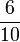 )
)
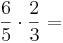 (!
(!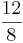 )
(
)
(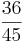 )
)
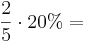 (
(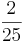 )
(!
)
(!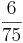 )
)
 (
(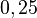 ) (!
) (!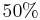 )
)
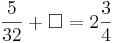 (
(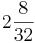 ) (!
) (!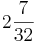 ) (!
) (!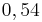 ) (!
) (!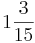 )
)
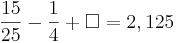 (!
(!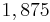 ) (!
) (! ) (!
) (!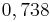 )
)
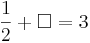 (!
(!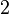 ) (!
) (!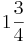 ) (
) (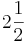 ) (!
) (!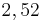 )
)
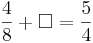 (
(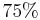 ) (!
) (!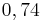 )
)
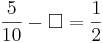 (!
(!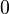 ) (!
) (!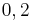 ) (!
) (!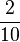 )
)

