Benutzer:Anna-Lena Friedrich: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Die Krokodilübungen zum Känguruwettbewerb)
(→‎Die Krokodilübungen zum Känguruwettbewerb)
Zeile 120: Zeile 120:
 
<br>
 
<br>
 
<br>
 
<br>
 +
 +
 +
3.Georg lebt zusammen mit seiner Mutter,seinem Vater,einem Bruder,einem Hund, zwei Katzen,
 +
  zwei Papageien,einem Pferd und vier Goldfischen. Wie viele Beine haben sie alle zusammen?
 +
  (!22) (28) (!24) (!32) (!13)
 +
 +
 +
4.Durch wie viele verschiedene natürliche Zahlen (einschließlich 1 und 24) ist die Zahl 24
 +
  ohne Rest teilbar?
 +
  (!4) (!5) (!11)(8) (!9)

Version vom 17. Februar 2009, 08:28 Uhr

Ich heiße Anna-Lena Friedrich und bin 12 Jahre alt. Im Regiomontanus-Gymnasium-Haßfurt besuche ich die Klasse 6a.


Meine Projektbeiträge


Wie viele Quadrate gibt es auf einem Schachbrett?


Nein, keine 64, auch keine 65 Quadrate.

Hier eine kleine Hilfe:


.....Bild..... 64+?

Schachbrett1.jpg


Lösungsidee

1. Schritt: 

3x3 Quadrat      3x3 Quadrat            3x3 Quadrat
9 kleine         4 sich überlappende    1 großes
Quadrate         Quadrate               Quadrat

2. Schritt: 

4x4 Quadrat      4x4 Quadrat            4x4 Quadrat
16 kleine        9sich überlappende     4 sich überlappende
Quadrate         Quadrate               Quadrate

Lösung durch Makieren des blauen Feldes sichtbar machen:

8²+7²+6²+5²+4²+3²+2²+1²=


Multiplizieren von Brüchen

Werde Multiplizier-Champion! Berechne und kürze vollständig!
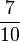
* \frac{1}{2} \frac{1}{5} \frac{3}{7} \frac{7}{10}
\frac{1}{2}
\frac{1}{4}
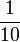\frac{1}{10}
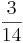\frac{3}{14}
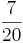\frac{7}{20}
\frac{1}{9}
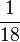\frac{1}{18}
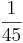\frac{1}{45}
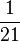\frac{1}{21}
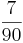\frac{7}{90}
\frac{3}{5}
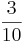\frac{3}{10}
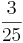\frac{3}{25}
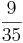\frac{9}{35}
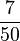\frac{7}{50}
\frac{5}{7}
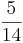\frac{5}{14}
\frac{1}{7}
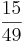\frac{15}{49}
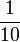\frac{1}{10}
\frac{1}{4}
\frac{1}{8}
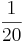\frac{1}{20}
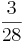\frac{3}{28}
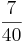\frac{7}{40}



Die Krokodilübungen zum Känguruwettbewerb

Die folgenden Aufgaben können nur eine richtige Antwort enthalten!

1.Wie viel ist 2000-200+20-2 ? (!222) (!1900) (!1902) (1818) (!1919)


2.Sabine und Sandro haben insgesamt zehn Bonbons. Davon hat Sabine zwei mehr als Sandro. Wie viele Bonbons hat Sandro bekommen? (!8) (!7) (!6) (!5) (4)






3.Georg lebt zusammen mit seiner Mutter,seinem Vater,einem Bruder,einem Hund, zwei Katzen, 

 zwei Papageien,einem Pferd und vier Goldfischen. Wie viele Beine haben sie alle zusammen?
 (!22) (28) (!24) (!32) (!13)


4.Durch wie viele verschiedene natürliche Zahlen (einschließlich 1 und 24) ist die Zahl 24 

 ohne Rest teilbar?
 (!4) (!5) (!11)(8) (!9)
Von „http://rmg.zum.de/index.php?title=Benutzer:Anna-Lena_Friedrich&oldid=13998“