Lernpfad zur zentrischen Streckung und den Ähnlichkeitssätzen/Ähnlichkeitssätze für Dreiecke - Ähnlichkeitskonstruktionen: Unterschied zwischen den Versionen
(→Aufgabe 1) |
(→Aufgabe 2) |
||
| Zeile 44: | Zeile 44: | ||
<span style="color: blue"> | <span style="color: blue"> | ||
'''Aufgabe:'''</span><br /> | '''Aufgabe:'''</span><br /> | ||
| − | Die Supermarktkette xy möchte in einigen Tagen eine neue Filiale eröffnen. Allerdings fehlt noch die quadratische Reklametafel an der | + | Die Supermarktkette xy möchte in einigen Tagen eine neue Filiale eröffnen. Allerdings fehlt noch die quadratische Reklametafel an der Fassade. Diese soll möglichst groß sein, damit die Kunden sie schon von weitem sehen können, darf aber aus Sicherheitsgründen nicht über den Rand des Daches überstehen. Der Werbebeauftragte Hans-Peter hat sich bereits die Maße des Giebels, an den die Werbung montiert werden soll notiert und möchte nun zeichnerisch die Abmessungen der Tafel bestimmen, damit er sie bestellen kann. |
Kannst du ihm dabei helfen? | Kannst du ihm dabei helfen? | ||
Version vom 29. Januar 2009, 08:08 Uhr
Manche Konstruktionsaufgaben lassen sich lösen, indem man zuerst eine Figur mit der "richtigen" Form, aber beliebiger Größe zeichnet und diese dann durch eine Zentrische Streckung so vergrößert oder verkleinert, dass die Größe stimmt.
Beispiel
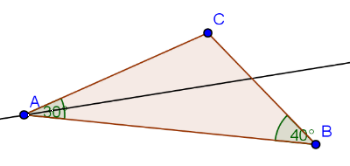
Aufgabe:
 = 30°,
= 30°, 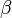 = 40° und w
= 40° und w = 6cm
= 6cm
|
Aufgabe 1
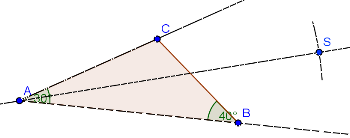
Aufgabe:
 = 50°,
= 50°, 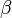 = 45° und sc = 6cm
= 45° und sc = 6cm
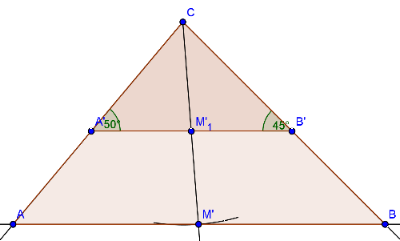
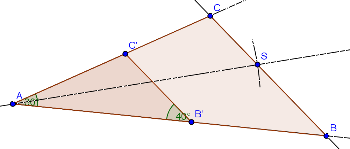
Wieder zuerst ein Dreieck A'B'C mit beliebigen Seitenlängen anfertigen und dann so vergrößern oder verkleinern, bis die Seitenhalbierende 6cm lang ist.
Aufgabe 2
|
Aufgabe: Kannst du ihm dabei helfen? |
Hier ein kleiner Tip
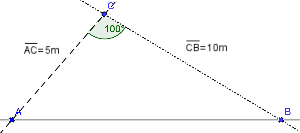
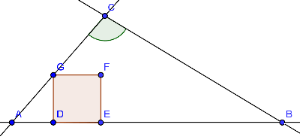
Zeichne zuerst das Dreieck im Maßstab 1 : 1000. Dann zeichne ein Quadrat mit beliebiger Seitenlänge ein, das das Dreieck mit einer Seite und einem Punkt berührt.
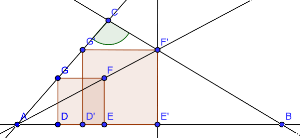
Und hier die Lösung
Jetzt musst du nur noch das Quadrat vergrößern und die Seitenlänge Abmessen und Umrechnen.
 Die Reklametafel muss eine Seitenlänge von 3,5m haben.
Die Reklametafel muss eine Seitenlänge von 3,5m haben.