HA: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde geleert.) |
(Änderung 8480 von Kundmüller Maximilian (Diskussion) wurde rückgängig gemacht.) |
||
| Zeile 1: | Zeile 1: | ||
| + | =Aufgaben zur Integralrechnung= | ||
| + | ==Aufgabe 1== | ||
| + | |||
| + | |||
| + | '''1.Bestimmen der Schnittpunkte:''' | ||
| + | |||
| + | f(x)=0; | ||
| + | |||
| + | a * x - b * x<sup>3</sup> = 0; | ||
| + | |||
| + | x (a - b * x<sup>2</sup>)=0 | ||
| + | |||
| + | --> Mitternachtsformel: x<sub>1</sub>= 0; x<sub>2</sub>= <math>-\frac{\sqrt{ab} }{b}</math>; x<sub>3</sub>= <math>\frac{\sqrt{ab} }{b}</math> | ||
| + | |||
| + | |||
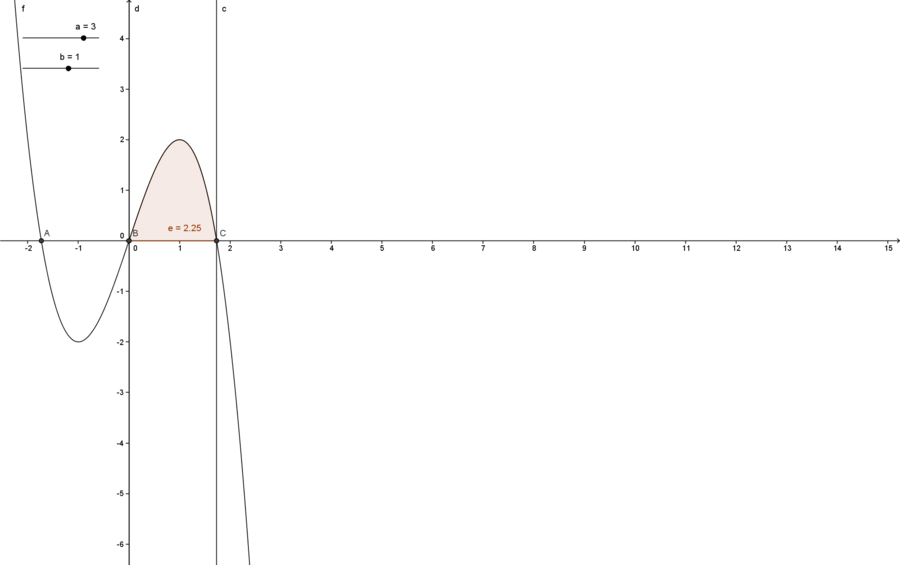
| + | [[Bild:Hausaufgabe_aufgabe_1.png|900px]] | ||
| + | |||
| + | '''2.Berechnung des Integrals:''' | ||
| + | |||
| + | F(x)=<math>\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx</math> = ... =<math>\frac{a^2}{2b}-\frac{a^2}{4*b}=\frac{9}{4} </math> | ||
| + | |||
| + | |||
| + | '''I.''' <math>\frac{a^2}{2b}-\frac{a^2}{4*b}=\frac{9}{4} </math> | ||
| + | |||
| + | '''II.''' f´(1) = 0 ; a - 3b = 0; a = 3b '''eingesetzt in I.:''' b = 1 → a = 3 | ||
Version vom 6. Oktober 2008, 18:50 Uhr
Aufgaben zur Integralrechnung
Aufgabe 1
1.Bestimmen der Schnittpunkte:
f(x)=0;
a * x - b * x3 = 0;
x (a - b * x2)=0
--> Mitternachtsformel: x1= 0; x2= 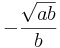 ; x3=
; x3= 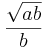
2.Berechnung des Integrals:
F(x)=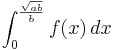 = ... =
= ... =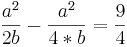
I. 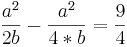
II. f´(1) = 0 ; a - 3b = 0; a = 3b eingesetzt in I.: b = 1 → a = 3