Diskussion:LK Mathematik 2008 10/Lösungen Infinitesimalrechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 12: | Zeile 12: | ||
F(x)=<math>\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx</math> = ... =<math>\frac{a^2}{2b}-\frac{a^2}{4b}=\frac{9}{4} </math><br> | F(x)=<math>\int_{0}^{\frac{\sqrt{ab} }{b} } f (x)\,dx</math> = ... =<math>\frac{a^2}{2b}-\frac{a^2}{4b}=\frac{9}{4} </math><br> | ||
Dann steht am ende folgendes bei mir: | Dann steht am ende folgendes bei mir: | ||
| − | <math> | + | <math>\frac{a^2}{4b}=\frac{9}{4} </math> |
<br>Daraus folgt auch wieder a = 3 (könnte auch -3 sein, was aber nicht mit a) stimmen würde), und b = 1.<br> | <br>Daraus folgt auch wieder a = 3 (könnte auch -3 sein, was aber nicht mit a) stimmen würde), und b = 1.<br> | ||
kappe | kappe | ||
Version vom 5. Oktober 2008, 09:43 Uhr
Warum kann ich keine GeoGebra-Datei hochladen???
- Du musst die Geogebra-Datei als .ggb abspeichern. Beim Hochladen musst du darauf achten, dass du den Zusatz .ggb der Quelldatei auch beim Zielnamen anhängst.
- Siehe auch folgendes Beispiel: Datei:Motorrad.ggb
- Zwei Beispiele wie man die hochgeladene Datei ins Wiki einbindet
- Hilfe zum Einbinden von GeoGebra-Dateien
- Gruß-- Maria Eirich 14:54, 3. Okt. 2008 (UTC)
Sers Baumi, bist du dir sicher, dass du dich bei "2. Berechnung des Integrals" nicht vertan hast?
F(x)=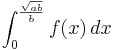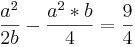
= ... =
ich hab hier immer:
F(x)= = ... =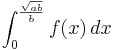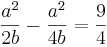
Dann steht am ende folgendes bei mir:
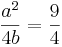
Daraus folgt auch wieder a = 3 (könnte auch -3 sein, was aber nicht mit a) stimmen würde), und b = 1.
kappe
