Benutzer:Greb Daniel: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 13: | Zeile 13: | ||
'''2.''' '''Berechnung der gemeinsamen Fläche mit Hilfe des Integrals:''' | '''2.''' '''Berechnung der gemeinsamen Fläche mit Hilfe des Integrals:''' | ||
| − | A= | + | A= <math>\int_{-4}^{4} g (x) - f (x)\,dx</math> = <math>\left[ 4x - \frac{1}{12} x^3\right] </math> "von -4 bis 4" = ... <math>\frac{64}{3}</math> = 21 <math>\frac{1}{3}</math> |
| − | <math>\ | + | |
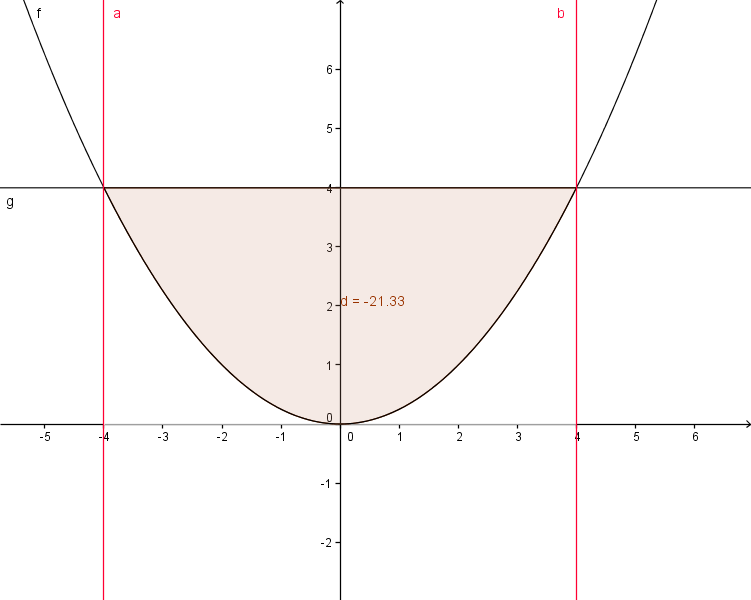
''Lösungsgraphik:'' | ''Lösungsgraphik:'' | ||
[[Bild:2117_neu.png]] | [[Bild:2117_neu.png]] | ||
Version vom 24. September 2008, 15:26 Uhr
Lösung von Christoph Wacker und Daniel Greb
S.211/7
Aufgabe: Berechne die gemeinsame Fläche von f(x)= 
x² und g(x)= 4!
Lösung:
1. Bestimmung der Schnittstellen der zwei Funktionen:
x² = 4;
x² =16;
x= +/- 4;
2. Berechnung der gemeinsamen Fläche mit Hilfe des Integrals:
A=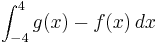 
= ![\left[ 4x - \frac{1}{12} x^3\right]](/images/math/c/9/0/c90ddde65c195eff53d8c1ebcb32f18f.png)
"von -4 bis 4" = ...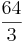 
= 21 
Lösungsgraphik:
