Hausaufgabe - Mathe: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (Die Seite wurde neu angelegt: Bild:10.png) |
|||
| Zeile 1: | Zeile 1: | ||
| − | [[Bild:10.png]] | + | '''Lösung der Aufgabe S.211/7''' |
| + | |||
| + | Gegeben sind die Funktionen | ||
| + | '''''<math>f(x) = 1/4x^2 | ||
| + | </math>''''' und | ||
| + | '''''<math>g(x) = 4</math>''''' | ||
| + | [[Bild:10.png|right]] | ||
| + | |||
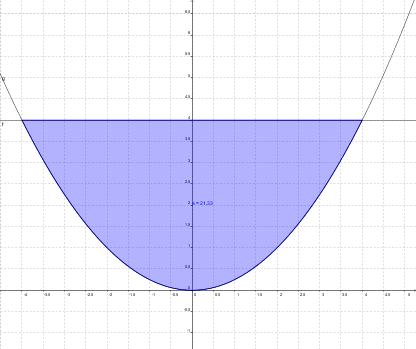
| + | 1. Die Schnittpunkte zwischen den beiden Graphen ausrechnen : '''''1/4x^2=4|*4 ---> 16=x^2 oder x=+-4''''' | ||
| + | |||
| + | 2. Dann muss das Integral der beiden Gleichungen von -4 bis 4 berechnet werden oder bzw. gleich das Integral von f(x) minus das Integral von g(x) gerechnet werden: | ||
| + | |||
| + | <math>\int_{-4}^{4} f (x) - g (x)\,dx</math> | ||
| + | |||
| + | 3. Wenn man alles richtig gerechnet hat xD sollte man als Integralwert auf '''21,33''' kommen. Dies ist dann gleichzeitig auch die richtige Fläche, da alles im positiven Bereich stattfindet!!! | ||
Version vom 24. September 2008, 15:02 Uhr
Lösung der Aufgabe S.211/7
Gegeben sind die Funktionen
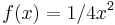 und
und
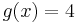
1. Die Schnittpunkte zwischen den beiden Graphen ausrechnen : 1/4x^2=4|*4 ---> 16=x^2 oder x=+-4
2. Dann muss das Integral der beiden Gleichungen von -4 bis 4 berechnet werden oder bzw. gleich das Integral von f(x) minus das Integral von g(x) gerechnet werden:
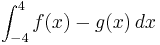
3. Wenn man alles richtig gerechnet hat xD sollte man als Integralwert auf 21,33 kommen. Dies ist dann gleichzeitig auch die richtige Fläche, da alles im positiven Bereich stattfindet!!!