Abi 2014 Geometrie II Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 24: | Zeile 24: | ||
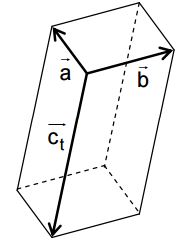
Die Vektoren <math>\vec{a} \begin{pmatrix}2 \\ 1 \\ 2 \end{pmatrix}</math> , <math>\vec{b}\begin{pmatrix}-1 \\ 2 \\ 0 \end{pmatrix}</math> und <math>\vec{c_t}\begin{pmatrix}4t \\ 2t \\ -5t \end{pmatrix}</math> spannen für jeden Wert von t mit t ∈IR\{0e} einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von t. | Die Vektoren <math>\vec{a} \begin{pmatrix}2 \\ 1 \\ 2 \end{pmatrix}</math> , <math>\vec{b}\begin{pmatrix}-1 \\ 2 \\ 0 \end{pmatrix}</math> und <math>\vec{c_t}\begin{pmatrix}4t \\ 2t \\ -5t \end{pmatrix}</math> spannen für jeden Wert von t mit t ∈IR\{0e} einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von t. | ||
| − | + | [[Datei:ABI2014 GII TeilA 1 Grafik.JPG]] | |
a) Zeigen Sie, dass die aufgespannten Körper Quader sind. | a) Zeigen Sie, dass die aufgespannten Körper Quader sind. | ||
Aktuelle Version vom 10. Juli 2017, 18:45 Uhr
|
|
Die Vektoren a) Zeigen Sie, dass die aufgespannten Körper Quader sind. b) Bestimmen Sie diejenigen Werte von t, für die der jeweils zugehörige Quader das Volumen 15 besitzt.
|
Eine Kugel besitzt den Mittelpunkt M (-3|2|7). Der Punkt P (3|4|4) liegt auf der Kugel. a) Der Punkt Q liegt ebenfalls auf der Kugel, die Strecke [PQ] verläuft durch deren Mittelpunkt. Ermitteln Sie die Koordinaten von Q. b) Weisen Sie nach, dass die Kugel die x1x2-Ebene berührt. |
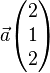 ,
, 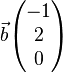 und
und 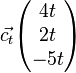 spannen für jeden Wert von t mit t ∈IR\{0e} einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von t.
spannen für jeden Wert von t mit t ∈IR\{0e} einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von t.