Abi 2014 Stochastik I Teil A: Unterschied zwischen den Versionen
| Zeile 84: | Zeile 84: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
| + | |||
</div> | </div> | ||
Aktuelle Version vom 8. Juli 2017, 14:15 Uhr
|
|
In Urne A befinden sich zwei rote und drei weiße Kugeln. Urne B enthält drei rote und zwei weiße Kugeln. Betrachtet wird folgendes Zufallsexperiment: Aus Urne A wird eine Kugel zufällig entnommen und in Urne B gelegt; danach wird aus Urne B eine Kugel zufällig entnommen
und in Urne A gelegt.
a) Geben Sie alle Möglichkeiten für den Inhalt der Urne A nach der Durchführung des Zufallsexperiments an. b) Betrachtet wird das Ereignis E: „Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A.“ Untersuchen Sie, ob das Ereignis E eine größere Wahrscheinlichkeit als sein Gegenereignis hat.
|
Betrachtet wird eine Bernoullikette mit der Trefferwahrscheinlichkeit 0,9 und der Länge 20. Beschreiben Sie zu dieser Bernoullikette ein Ereignis, dessen Wahrscheinlichkeit durch den Term |
Die Zufallsgröße X kann die Werte 0, 1, 2 und 3 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von X mit p1, p2 ∈[0;1].
Zeigen Sie, dass der Erwartungswert von X nicht größer als 2,2 sein kann. |
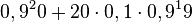 angegeben wird.
angegeben wird.

