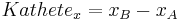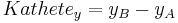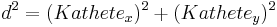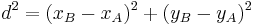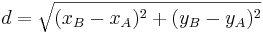Der folgende Hefteintrag fasst das obige zusammen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> <span styl…“)
 
 
Zeile 20: Zeile 20:
 
*<math>d=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}</math>
 
*<math>d=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}</math>
 
|}<br /><br />
 
|}<br /><br />
 +
 +
 +
 +
Aber nicht nur in der Ebene kann man den Satz des Pythagoras anwenden, sondern auch in der Raumgeometrie.
 +
Dazu fährst du fort mit Kapitel 5!
 +
 +
[[9d 2014 15/Raumdiagonale|5 Raumdiagonale]]

Aktuelle Version vom 3. Dezember 2014, 17:26 Uhr

Arbeitsauftrag:

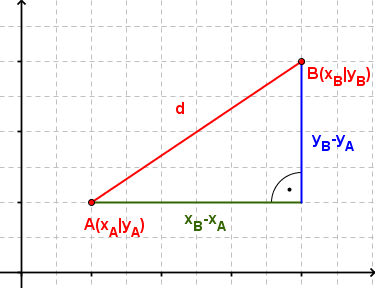
  • Zeichne die Grafik in ein Koordinatensystem
  • Notiere dir darunter die einzelnen Schritte zum Berechnen des Abstandes zweier Punkte


Abstand allgemein.png
  • Idee: Berechnung des Abstandes über den Satz des Pythagoras

  • Eintragen eines rechtwinkligen Dreiecks in das Koordinatensystem

  • Bestimmen der Länge der Katheten:
  • {Kathete_x = x_B - x_A\,}
  • {Kathete_y = y_B - y_A\,}

  • Anwenden des Satzes des Pythagoras:
  • {d^2=(Kathete_x)^2+(Kathete_y)^2\,}
  • {d^2=(x_B-x_A)^2+(y_B-y_A)^2\,}
  • d=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}



Aber nicht nur in der Ebene kann man den Satz des Pythagoras anwenden, sondern auch in der Raumgeometrie. Dazu fährst du fort mit Kapitel 5!

5 Raumdiagonale

Von „http://rmg.zum.de/index.php?title=Der_folgende_Hefteintrag_fasst_das_obige_zusammen&oldid=61184“