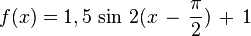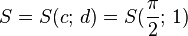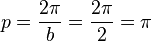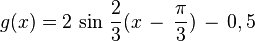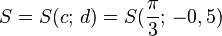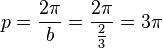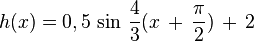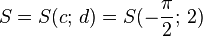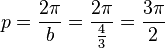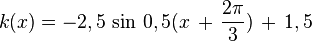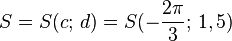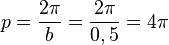Graph zeichnen: Unterschied zwischen den Versionen

Version vom 9. November 2014, 18:58 Uhr

Übungen zu y = a sin b(x - c) + d

Bewege die Punkte S ("Start"), P ("Periode") und B ("Berg") mit der Maus und zeichne so die Graphen der folgenden Funktionen!
Du kanst Dein Ergebnis kontrollieren, wenn Du Dir den entsprechenden Graph anzeigen lässt.
Wenn Dein Graph nicht mit dem vorgegebenen Graphen übereinstimmt, hilft es Dir, Deine(n) Fehler zu finden, wenn Du Dir die Funktionsgleichung zu dem von Dir eingestellten Graph anzeigen lässt.
Wenn Du Deine(n) Fehler auf diese Weise nicht findest, kannst Du Dir die Koordinaten des Startpunktes S und die Periodenlänge anzeigen lassen.

$f(x) = 1,5\,\sin\,2(x\,-\,\frac{\pi}{2})\,+\,1$	Startpunkt [Anzeigen][Verstecken] $S = S(c;\,d) = S(\frac{\pi}{2};\,1)$	Periodenlänge [Anzeigen][Verstecken] $p = \frac{2\pi}{b} = \frac{2\pi}{2} = \pi$
$g(x) = 2\,\sin\,\frac{2}{3}(x\,-\,\frac{\pi}{3})\,-\,0,5$	Startpunkt [Anzeigen][Verstecken] $S = S(c;\,d) = S(\frac{\pi}{3};\,-0,5)$	Periodenlänge [Anzeigen][Verstecken] $p = \frac{2\pi}{b} = \frac{2\pi}{\frac{2}{3}} = 3\pi$
$h(x) = 0,5\,\sin\,\frac{4}{3}(x\,+\,\frac{\pi}{2})\,+\,2$	Startpunkt [Anzeigen][Verstecken] $S = S(c;\,d) = S(-\frac{\pi}{2};\,2)$	Periodenlänge [Anzeigen][Verstecken] $p = \frac{2\pi}{b} = \frac{2\pi}{\frac{4}{3}} = \frac{3\pi}{2}$
$k(x) = -2,5\,\sin\,0,5(x\,+\,\frac{2\pi}{3})\,+\,1,5$	Startpunkt [Anzeigen][Verstecken] $S = S(c;\,d) = S(-\frac{2\pi}{3};\,1,5)$	Periodenlänge [Anzeigen][Verstecken] $p = \frac{2\pi}{b} = \frac{2\pi}{0,5} = 4\pi$

@@ Zeile 29: / Zeile 29: @@
 <br>
+<ggb_applet width="750" height="436"  version="4.2" ggbBase64="UEsDBBQACAgIADmXaUUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIADmXaUUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVpbb9s4Fn7u/ApCD4tkGju86NrYHSQz6O4AaRtMuovuIi+URMusZcmR5MQp+rD/cP/SHJKSLNuJx4mbbdDYFMVDnvt3SLqDXxbTFN2IopR5NrRIH1tIZFEeyywZWvNq1POtX97+NEhEnoiw4GiUF1NeDS27T63lPOj1Xawmy3hoMRKLkAZ2LwhGTs+O4rDHBQt6LLD9KMae7WDbQmhRyjdZ/oFPRTnjkbiMxmLKz/OIV3rNcVXN3hwf397e9hvu/bxIjpMk7C/K2EIgeVYOrfrhDSy3MumWaXKKMTn+/P7cLN+TWVnxLBIWUlrN5dufXg1uZRbnt+hWxtUYbMBc10JjIZMx6Ol4zELHimoGys5EVMkbUcLcTlcrXU1nlibjmRp/ZZ5Q2upjoVjeyFgUQwv3KWMO9R0HO4TatkMslBdSZFVNS2qex81qgxspbs2y6klztHHggQ9kKcNUDK0RT0tQS2ajAkwKAhVz6JbVXSpCXjT9pTzkCP4Bgfwq1FrgO2MHGMH4SH08+ICIRpYuYwtVeZ7qVTFyAvTtG6KYYnSkGmIaCo3rmiFs3mFmGmoa2zSOobHNdNuQ2obGNjQ226Jn3V8qWr9Y0bTRk3b1xEf4CBQ/0sqv6eh3dCRKgW+IKMl1w5CSmWjZVWPXXdd0Pd0QbBpSD/rqS9vK3VMb1mjD7vOa+4BGpMPVxMLDTDdipeFImLOjAeleSrIHHUYfUm9Pq7YadhV0IAHUn/5ssGSP0vFhm+7O0bX3SfgnMPTw/4Ph4LiBt0GddKgcK9o6TisxLRXUsECjDSLIgYx0PQAHB5EAGk9lJkXEQbYDXeIjV7UeYioZbcSQjxQdYUhjiuPDl60T1UUOrKVeeiZjEbORwxDRSGQjwB+k0QyQjTKgcBzkwCTFnSi2zEW2Cx3mIxsEVDjmKbxgMA/6wJwiRhBTc4mHqItcijyFhcRWEOn6SnZYlCIXI1dNBTAEIDQgCDN8xJQ2EOGzvJStcccinbVe0XaU2WxerdgumsbNY5WvUcd5NDlrbV2PCF5WXTKoQctKZ2rSSiF8NUh5KFLYL1yqQEDohqcqfzWHUZ5VqAkCat4lBZ+NZVReiqqCWSX6wm/4Oa/E4h1Qlw1vzVoX6IGYR6mMJc/+BVGillALomW9VtHV1Gsb+4ZNlOdFfHlXQuygxX9EkSsJvL7j2R6jfuDBR+XvnRmi2O+7FDMWOJ6PHS9wIHYjrqLepn2HEOYBG9fxCQ1gUjNkw5AXEJjn4oAEtm14i5tWOb4QZeOApJBx9/n38ixP49bYs1xm1a98Vs0LvfsCDCyUUqdZkgptXI2qsI+JJmG+uKwB2az16W4GPWz4h8mveZoXCHKSOqBJUrehaTWNEqylwpoGawrcuEnG7TgJqKbQbWhaTQV+N6LVipJGS4obNrLUSAKLd+NSB43aFM0zWZ03nUpGk1pTYug/zKchxFsbw0DwmzRbOLVddTzsBS6jrgd7ywA2bqtMybMw7VgI9nRl9Vnt6BzKnMD3PAe+aeD7lh76tx4yz5/GouL3kupYX4vywUQUmUhNKGcQTPN8XprkahPk1WBeigtejU+z+A+RAC5ccAXNFQhvSLUCJtlFJKcw0byv3cdVaP0TjGHexiIpRE3PU73lNs7Vo7ibWBuv9VLvinz6e3bzCeJ2TdTBcaPPoIwKOVPZgUKoFROxzACwEodKE3fngfIlaBEp1ANPVMpNFuLzapwXelMNyDG0AvQhvxHKawDXxLYUaixmhSjV+cT4HQ2tBOBtASCYHCwO0RDqxc+ATdkBRcdQIH5GBwvUQ6xPbOIE1HWYAzARMDV4eAgjypFKIpGKKWzVUaVTbjTPtGxtdCX6GKDCCOXhF8DJtehbugRUizWa66D7WBNPzSDM3UjiJkERT2djHUq18VN+B5p33aGZfRyNSlGhhVoBUAtqb2fwfR6venAkFyJeD5tlglcA2hM4jZTmAKCVhyzXT/+QcSx0UTKhbCy0YSuNcK0hLnc2VNcWXajSdnm0LXpKajBGj5Bt5uAZ5IvxTiVmioFCh5kQBleMRvAwA4YarztpqXOkVMz0ofiubr920EPbQmH4SsE0b9eSq2vQKJ9OeRajTO/AzsE71rLwc6ysijgZWotTwMDaevOqGZRmuXqRDf8oZ7fml5vuaXbNu/pn90jdsP6mBUltwd5yrftikzauuS80oTRfZ2ZKaRBfTmepjGS13c4XOnBXDS03rHux3bqr0X/xpOgn1CCBbp+eAcQ3GWA/fwK4fRpg13M814W9E9Z7ru+XDusgDzWsxvi7g8tDs4Fd9UI2n4pCRtaSXl+v8HTe8GhE2iWqNwFvQ6CoFmixo0DRcwsU1gKp8qeqHRS4g8XBhSpxSsadhAw3hQwCn2EaUEpx4NrM/a4yn9YyHygJ0WvUyL5eqUP42EfozuixknebSq0m5OnT8E4dyRPThKbZH/LUvpbZruuCLR2GnWesIB8L2EglecbTe2rJqaklm0iXPqKOpC+kjvTIRiles/ILKCrphqnPHlNUzn5gUTFR2mPPX1LuTQ/ybBWFtxXlTGHkroWFr0Mk+c44fl3LdW1OM7w+zYTNSSY6VEgZ3yfrxqHl+i8Cp+OHlYMJtrvbcbwH+m0/aPzlOWPDOpVYVKS20N+u53l18psAFlcn7+bZROn+Bl2dwN/VyZ16GF6dGCowGYdP3bk6AZOizljYjh0srk56VycH7dBBpI6KUJQOW5r//ffw8OrkdZcqbgcPTXOff5Tw1qom+x0q82cDWFme80/i8/q5Ud/8lZAQo+VVOOTi+zpRzZUgthrEbPAhLPN0XonLqBAia34LRCrpmfqRDPKcmUuebc6Hk/6o9vzI5AYgRnvWr7MD61cbewidM2SXc/5oT5c8WPOaq7qnnPPtoN7YBz/2pB/meSr40lhiHQw7gLLPDcBTbETqSKKBt3XnUN+zIm2tFX/ymfampv67us5GN9DVscazr0ImInuceaYv0DyMbI2hR5sn2WqezRQe1yk8NimM2xS2l9d1r5sDDNV5S3fJ2/GeefvlOe6kqFvvnujLytsvLzEw7a33do8OzPEjA3NSB+bEBGaPtpFpYlTHZedwXdeU3W6PJ3tGZ/YMdmcmNn/w5fF6aGYvMTTdrcefR4fm5OklJX9B5mE0+I6Z22zgyyQVMhrPswR9nU8R7O4TAcfKNK1EhowNHzLdcfdXJf1Dc/0/zN7+CVBLBwgigdh5bQkAABEnAABQSwECFAAUAAgICAA5l2lF1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIADmXaUUigdh5bQkAABEnAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAABAoAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 </td></tr></table></center>
 </div>

Graph zeichnen: Unterschied zwischen den Versionen

Version vom 9. November 2014, 18:58 Uhr

Übungen zu y = a sin b(x - c) + d

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Hilfen

Oberstufe

Studien- und Berufsorientierung am RMG

Werkzeuge