Übungen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→y =) |
(→y =) |
||
| Zeile 80: | Zeile 80: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
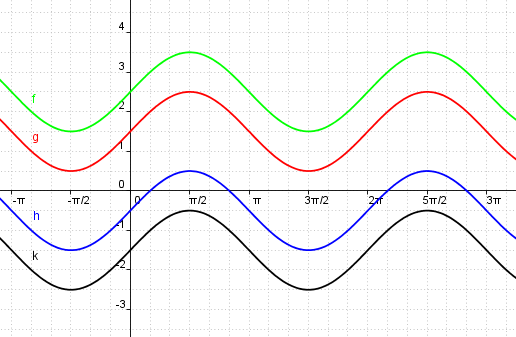
| − | == y = == | + | == Die Funktion y = a sin b(x - c) + d == |
| − | + | <ggb_applet width="889" height="504" version="4.2" ggbBase64="UEsDBBQACAgIAGWNaUUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAGWNaUUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VzrUuNGFv6dPEWvtyoFG2z6otZlgKQg2exO1RCohUllt/gjS42tQZY8kgxmkqnKw+RN8gB5pT3dLdmSb0jYZjzJxLSlbnWfS5/vXNRw/O14EKJ7kaRBHJ20SAe3kIi82A+i3klrlN227da333x53BNxT3QTF93GycDNTlpGh7amz8FVx8Ty4cA/aXmCY4qJ1zaZa7UN36JtWxhumwjT9Ihn3gpqtxAap8GrKP7RHYh06HriyuuLgfsm9txMzdnPsuGrw8OHh4dOsXonTnqHvV63M079FgLKo/SklX95BdNVHnpgajjFmBz+fP5GT98OojRzI0+0kORqFHzz5RfHD0Hkxw/oIfCz/knLwbyF+iLo9YFN0yAtdCgHDYHXofCy4F6k8GjpUvGcDYYtNcyNZP8X+hsKJ+y0kB/cB75ITlq4Qyl2HMOwOGE2oYQbLRQngYiyfHCx6GEx3fF9IB70vPKbWtLAjgU6CNKgG4qT1q0bpsBWEN0mIFKgKBnBZZo9hqLrJsX1lCByAP9gQPBByLlAd1oOJy3G2IHtHFgYH3CONSnldVsoi+NQTYoRd9CvvyIKCkcHsiG6odCYpu7C+h5muqG6MXTD9RhDP27ooYYeY+gxBlvBZn495TO/UWG0YJOW2cQH+AD4PlC8z/Bol3gkkoFfEZGUq4YhSTNRtMvGyC9NfWmphmDdkLzTlj+UrMw1uWEFN6zMDcx+ID/mEo5IaVW9FZYvOrdVihVt26knP7oWj2ypvugy7tYUarEg4aUFOex/+b/6zC3JGvG4VKTE4HVXNI11zP0ZLFr4JRY8PizA7Ti3OZT25dh8m2ZikEqkYY4CG0QQB4M0LcAGjogDjSUNkyLCkcHhktjIlK2FmLRFAzFkIzmOMKQghdvww1B2aiIOc8mbljZYxAzEGSIKiAwE8IMUmAGwUQYjOEccHpKrE7ksM5FhwgWzkQEEShizJFwweA6uYXGKGEFMPkssRE1kUmRJKCSGREjTlrTDpBSZGJnyUcBCwEGNgfCEjZjkBnb4ME6DiXD7IhxOtKLkGETDUVaRnTfwi69ZPDPaj727s4ms8x7hpll5GHigqaPTHqniB784Dt2uCCFauJIbAaF7N5T2q1a4jaMMFZuA6nu9xB32Ay+9ElkGT6XonXvvvnEzMf4BRqfF2mqsF0fpZRJn38XhaBClCHlxiCesxSEpfacTquGClTqMcgcvdZil79bCdWPoQaNUwPpxkhbDXd9/LUdMjRwEeBGFj2eJcO+GcVBl4/hQRRnHYuSFgR+40U+w2eUqUi6oCDoUsBZBh2GZBSFx4l89pmABaPw/kcRSjlaHW4bFqO1Y8GGAHo+6i2K7Y1LMmMMtG3PLga7Uc6XtGrTDCWEW49jkNgF8fSx6DOixHAKPmdgh8IxaWdxPFOSOxYT3XhL45e+v07M49CeSUMx/5w6zUaLiR1gnkSydRr1QqA2iPANEYt5dNx5f6Z3B9FzXj0O4wnr9bk8JHQGuUA589PK2q1s1RhI2GYXVGKxG4GKrBf6knzhUjVBtV7dqFOxdTVrOKCm4pLhYJkgVGuJWxbbUxpdx3SgKsjfFRRZ4dzmnRI//cTToiun2kQO+D3QQKgNubmHLMRk1LcewHdOcWZRsZdGShCAsTbOfZVDKKeOObVkcflLHtluq67+qS3+/7ovMXThUbfSZLX58J5JIhLlFwWYaxaNUA0TJ2MC+Lt2sfxr5/xE9wLZLV7qXDIjXQxUDGrCEFwzgQX0/V58rt9ZbEIa+64teIvLxbqiSBq1c1YvLZjV3W031QxIPXkf317BvZ0g9Piz4OU69JBhK60Bd8Hd3YmoBICUXvKVffk6CBXDhSeQGTWRSTQAjo6wfJyovAPSDtAP9GN8LqTVwOcRoScgIxQByApQpy1DGNdkBVyrbkKpGcfcd4PHMDpmKDZb3ldfQQJUPTnQnPLvQhJSxueGwr9SdCyh0H4G6ssjUYhe3t6nI0Pik1SaQkDxCa5a6z2N/Vs6gRk1QJoZyfrlph0Lo7a65hS9DWE/BSAWaQXWpXGuB5cilqUxCP5T2uBKbRJqKa9J3Z7YA7GAtcaW0wcCNfBSpWOcNgERr6mJdLBWAXHBA41Ow1FyWo6zoDPR0+SRzqpSYM9FUMK/JIj6dVeUybeHauppTxlSgKn1/zGsAIME2ncw1gcgMXPcdZKSpwvEsR2z15d+B7wsVmWgH8j7Sj6Qal4LBMAy8IFst50u1x6uCDuake7laulVDudxNQ+HaUIwXMBTccRxOHfDxEBdYMrjYpKGI8TCBDSGpzCX6AGHkGMgd713uozYa713t61iyqqZoNBBJ4LWmj6k6hxuO8qWcjkENjqll2Y5DuV3fBsjTRPo5kY81qfNnqZtYx4YI8iZSq0eQN0vQslBiQ/R1c/oo+gdiHchdDtFeScO1aO7O0ow7pmkyw4YU0cEWNpi1UZpPc5r3JIXoa1TQTrhDTc44hNAOA0a68DEO0KPmo4Ii80xV4eX0CXipphUL8GWwjOMi3q0P7lN8cTSS1wN+1nGoTYiFbQoqIJAhbNGTXiQQ9vTiyA0X+NRT7VPnET9s4E/DHfGnbZI7VJwLcoGcd8C9hnPCPmviXs/WdK/9eU0QqhM+1T7bxVLtYFfawGYc7BL7YR3D4QDFzICs23awzHO34m/diSs7k2hc16O58w5kjuBNgvH7nMz3e+N9dIJcwOI0iPa60O6NgW5vX0K0v4j021GksqfWdK7aqFumnmKjHLrJq+fa+UKjNVYZ7WrpZGKckVxCX70fxdnRI7o5Qic3R/oKROPCJ7+4OQLRoVJfd9K3N745at8c7U269jzwbtLr7U/G/Pnb/v7N0dflUf6kc183i/QgiWxVKV7P+uOt4XCQvnGvxc+zNQRVkkzBDm6n5TswwfM87dG1StwqYDVHD7ebxuEoE1deIkRUvKJECmaoTnkN7swpuSK7bhyHwp1u4XjW/Ep7to5A15fZFCsJ12hpsNUhQ163Q7fBWPgV7bpDJRE1+odRdCev0l4oAq8/inrow2iABCCoAJwNw0xE6F+yDvyqcdZ9tirrFg2iBLFu3LbAcT03bmuSlC/wKsvxiBV4RDcZRTQthtw2UMvtFtRSFJA/Xa1kogeZ9q+hh3m3cT2T4ZjT7KyU1IB3dZsmNtebD+xM7X1l09XN+pqwOyZziMUMQjBzGMsjbg65JIVIzDQcgh3bepma4PUqM+g1MIPeZ4pOCwS/fXRa7Wf7s352unE/lZulnK2Ubz03SzroyusnQZbNudHF4SWthJdnIum1YQ8HAo1gT1+7ob7Ko78awR/dPEJsbI8q0b1A8GdrhVo10jQpMlZRAUREH2SEFEE8lMYPoAm/ifzZtuS/tqNcKP0VcmRmQzkaFTmegw1AWOn2GgjP2LzwNhZnvMzmNRxeX+jnRZyBn1cmPd9CmXSLcd12ap9XoifvL05pTucChnerA4Y0n60Q4bsdqkSvEPGCKlO5SNrmHdviFDMuX2IYjuU8t96yOoBQkg5lVe91JA8bCFVgmj+ecCfEUJ5MuYiuEzdK5fHnqmU+DVZmBaz8m6NyUWdhvWsOrcw10Wqb1rMQrV6q/MJsKwex+fLLQmXYFWW4VWW4tZRhb14Z2417XkoZ3OBLlbEyRh/sYIxu8ZV4Vi9Gp01jdF7ZnqfdUKQQHPpA82P7J4Aprx+I7ijq1Q90+LZ264tHiZNoWx/de1qYVkWYMsuRgjyVXiAb+Q2CResvI0ODOfVl+LZcXDpAuGnQ93bdiORuKVJiY/1XOE+eJcMvGAXmFdS3c1Fg1CwKjD4XmdOZt+PtuYMZdUpHZEcivwYqvpxT8bCZiodrotFSDa93oo3ot97NEq25M15qKxC7A6E/xpxDFmBzYq7YCjuXA6yMdJIdjHQca6XO6kU6bEWks8JFXOxyXWAzx0PwDNBt1pv8BFKIkxmkudBIcz6HNPerkeZeT1YI/36XlbO8aDOd6hl4UfrdgBwxPDfJRBq4UW6mGVyrg1Q6OLqoF4s6lVj0Sk6CrupHoM7unGL+ZLV2nekzYtSTOKkep7kEWoDyqP3PCOi/rC96su4hl7+Q7PX53Pru7m733B0z6EpYqefujKaJPWFLM/vxMzN7su4LoCcCwRdN7XXGxRacoloszuobIK9ax5sceavkE+Xzb03OuK37qmi7GdVOlF+ZYdbUW7UmM5zR28OCo4pNVLVuoWaDqdFuKYrbdq4oXlNR9uxpAeH1I8Cnm6P7OLo56r66mbjU8I/fo564OZL/tEbRzW3ier/QP3/7+Ev3I2qAaesW118Y0zajP1wfIM26+que9tiL/vjd60MakyDIYDMR9EQkfc/3o8Tr99yot49KpxEa6GvdQyBPBEcveQiB8qVBzmIR46qIFwsW+fKbPNmBpucU9uWZmwZSxn8ZKVOLNgzjzYVV/Cr2NBDluq9SdydoMjhvGDRV3y4tOKftjlKQ7kCfzkZdkWbBYNAID+q/btqGBFfALpv5b/KXrxp4UfWHutQBvnoCp1WE+H6E7twIUEKhwaUUv/jq7wQfXaG9r9xhnB7pn6o6UL6xf6CGXVaHVTLaynCFLvKJs+oT8sxfZaAaNAgyZVLnUvv3RSoior81OAr4FEA9WSra3m+CbCJFpk8bY36aSv5xqnrGWK0InYZp/EqHUN25EGr4Ud/K7yG4iT7+sjps/jgTWpd+b/dh4e+HzdvyukWnzzIWq1MNyWMxZ86F1a/Nzr/oGzWqzY4+l/d8T7xb/cTF2sPyH2eR18Wfmvzm/1BLBwjGMcu3/w0AABpTAABQSwECFAAUAAgICABljWlF1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAGWNaUXGMcu3/w0AABpTAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAlg4AAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | |
<br> | <br> | ||
| Zeile 95: | Zeile 95: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| + | |||
== y = == | == y = == | ||
Version vom 9. November 2014, 17:45 Uhr
Die Funktion y = a sin b(x - c) + d
|