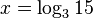Gleichungen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Teste dein Wissen) |
|||
| Zeile 12: | Zeile 12: | ||
== Teste dein Wissen == | == Teste dein Wissen == | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | {'''Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen.''' <br/>Gibt es nur eine Lösungen, trage in das andere Feld "-" ein.<br/> | + | {''' Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen.''' <br/>Gibt es nur eine Lösungen, trage in das andere Feld "-" ein.<br/> |
Gibt es zwei Lösungen, so ordne diese der Größe nach.<br/> | Gibt es zwei Lösungen, so ordne diese der Größe nach.<br/> | ||
Ist das Ergebnis 0, trage "Null" ein. <br/> | Ist das Ergebnis 0, trage "Null" ein. <br/> | ||
| Zeile 32: | Zeile 32: | ||
<math>x= \log_{3}{15}</math> | <math>x= \log_{3}{15}</math> | ||
</popup> <br /> | </popup> <br /> | ||
| + | <br/> | ||
| + | |||
| + | '''2. Löse das folgende Gleichungssystem: '''<br/> | ||
| + | |||
| + | (Ι) 2x+2y=9 <br/> | ||
| + | (ΙΙ) 1−6x=2y | ||
| + | <popup name="Lösung"> | ||
| + | Mögliche Lösungsverfahren: Einsetzungsverfahren, Gleichsetzungsverfahren, Additionsverfahren<br/> | ||
| + | x=-2 ; y=6,5 | ||
| + | </popup> <br /> | ||
| + | <br/> | ||
|width="5%"| | |width="5%"| | ||
|valign="top"| | |valign="top"| | ||
| + | |||
== Knicktests == | == Knicktests == | ||
<br/> | <br/> | ||
Version vom 2. September 2014, 18:21 Uhr
|