Catalanische Körper: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Allgemeines) |
(→Triakistetraeder) |
||
| Zeile 75: | Zeile 75: | ||
<center> | <center> | ||
<popup name=""> | <popup name=""> | ||
| − | [[File: | + | [[File:Triakistetrahedron.jpg|x200px]] <font size="7"> « </font> <font size="6">=</font> <font size="7"> » </font> [[Datei:Tetraederstumpf waagerecht.png|x200px]] |
</popup> | </popup> | ||
</center> | </center> | ||
| Zeile 81: | Zeile 81: | ||
<span style="color:#000000"> | <span style="color:#000000"> | ||
|} | |} | ||
| − | |||
| − | |||
== Rhombendodekaeder == | == Rhombendodekaeder == | ||
Version vom 12. November 2013, 00:33 Uhr
|
|
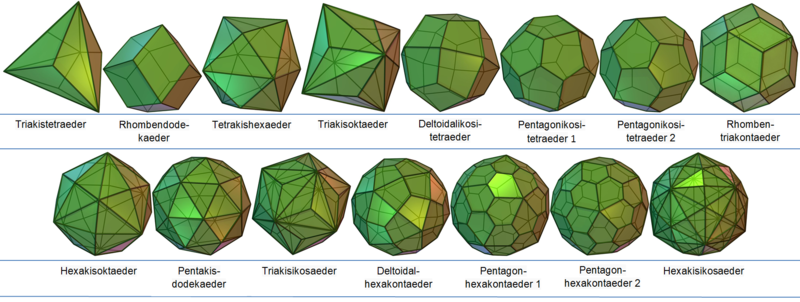
AllgemeinesBei Catalanischen Körpern wird die "Oberfläche aus kongruenten ungleichseitigen [...] Vielecken einer einzigen Flächenart gebildet"[1], die "Ecken [werden] von ungleich vielen Kanten gebildet"[2] und die "Kanten [sind] ungleich lang" [3].
Triakistetraeder
Rhombendodekaeder
Triakisoktaeder
Tetrakishexaeder
Deltoidalikositetraeder
Großes Rhombenkuboktaeder
Rhombentriakontaeder
Triakisikosaeder
Pentakisdodekaeder
Pentagonikositetraeder
Deltoidalhexakontaeder
Großes Rhombenikosidodekaeder
Pentagonhexakontaeder
|