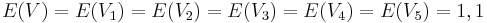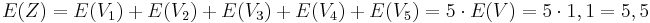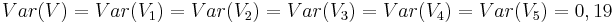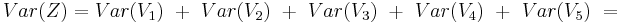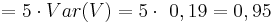2010 III: Unterschied zwischen den Versionen
K |
|||
| Zeile 176: | Zeile 176: | ||
Varianz von V. | Varianz von V. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | V: Verzögerungen in Sekunden<br> | + | ''V: Verzögerungen in Sekunden<br>'' |
<u>Berechnung des Erwartungswertes:</u><br> | <u>Berechnung des Erwartungswertes:</u><br> | ||
| Zeile 189: | Zeile 189: | ||
<math>Var(V) = (0,5 - 1,1)^2\cdot\ 0,2\ +\ (1,0 - 1,1)^2\cdot\ 0,5\ +\ (1,5 - 1,1)^2\cdot\ 0,2\ +\ (2,0 - 1,1)^2\cdot\ 0,1 = 0,19</math><br> | <math>Var(V) = (0,5 - 1,1)^2\cdot\ 0,2\ +\ (1,0 - 1,1)^2\cdot\ 0,5\ +\ (1,5 - 1,1)^2\cdot\ 0,2\ +\ (2,0 - 1,1)^2\cdot\ 0,1 = 0,19</math><br> | ||
<br> | <br> | ||
| − | |||
| − | |||
}} | }} | ||
<br> | <br> | ||
| Zeile 200: | Zeile 198: | ||
voneinander angenommen werden. | voneinander angenommen werden. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | + | ''Z: Zeit in Sekunden vom Umschalten der Ampel auf Grün bis zum Anfahren des fünften Autos in der Schlange'' <br> | |
| + | <br> | ||
| + | '''Berechnung des Erwartungswerts:'''<br> | ||
| + | <br> | ||
| + | Alle Autos <math>i \in \{1,2,3,4,5\}</math> besitzen die gleiche mittlere Verzögerung <math>V_i</math>, die jeweils gleich dem Erwartungswert von V ist.<br> | ||
| + | <br> | ||
| + | <math>E(V)= E(V_1) = E(V_2) = E(V_3) = E(V_4) = E(V_5)= 1,1\ </math><br> | ||
| + | <br> | ||
| + | Somit folgt: | ||
| + | <br> | ||
| + | <br> | ||
| + | <math>E(Z) = E(V_1) + E(V_2) + E(V_3) + E(V_4) + E(V_5) = 5\cdot E(V) = 5\cdot 1,1 = 5,5</math> | ||
| + | <br> | ||
| + | <br> | ||
| + | '''Berechnung der Standardabweichung:'''<br> | ||
| + | <br> | ||
| + | Alle Autos <math>i \in \{1,2,3,4,5\}</math> besitzen die gleiche Varianz <math>V_i</math>, die jeweils gleich der Varianz von V ist, da das Anfahren der Autos als unabhängig voneinander angenommen wird.<br> | ||
| + | <br> | ||
| + | <math>Var(V) = Var(V_1) = Var(V_2) = Var(V_3) = Var(V_4) = Var(V_5) = 0,19\ </math><br> | ||
| + | <br> | ||
| + | <math>Var(Z) = Var(V_1)\ +\ Var(V_2)\ +\ Var(V_3)\ +\ Var(V_4)\ +\ Var(V_5)\ = </math> | ||
| + | <br> | ||
| + | <math>\quad = 5\cdot Var(V) = 5\cdot\ 0,19 = 0,95</math> | ||
| + | <br> | ||
| + | <math>\sigma(z) = \sqrt{Var(Z)} = \sqrt{0,95} \approx 0,975</math> | ||
}} | }} | ||
<br> | <br> | ||
Version vom 5. Februar 2011, 00:25 Uhr
|
|
An einer Ampel stehen Autos hintereinander. Die Ampel schaltet auf
Grün. In einem einfachen Modell geht man davon aus, dass ein Auto erst
nach einer gewissen zeitlichen Verzögerung gegenüber dem Auto anfährt,
das in der Schlange vor ihm steht. Für die möglichen zeitlichen Verzögerungen
sind in diesem Modell vier verschiedene Werte vorgesehen. Die
folgende Tabelle gibt an, mit welcher Wahrscheinlichkeit sie jeweils
eintreten.
Diese Tabelle gibt auch die im Modell möglichen zeitlichen
Verzögerungen zwischen dem Umschalten der Ampel auf Grün und dem
Anfahren des ersten Autos sowie deren Wahrscheinlichkeiten an.
V: Verzögerungen in Sekunden Berechnung des Erwartungswertes:
Z: Zeit in Sekunden vom Umschalten der Ampel auf Grün bis zum Anfahren des fünften Autos in der Schlange 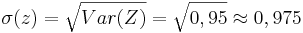
|
Durch eine Befragung soll der Anteil p der Pkw-Halter abgeschätzt
werden, die bereit wären, ein Elektroauto zu kaufen, wenn dies vom Staat
mit 2500 € bezuschusst wird. Dazu werden 1000 zufällig ausgewählte
Pkw-Halter befragt. Wer mit „Ja“ antwortet, wird als Elektroautokäufer
(kurz: EAK) bezeichnet.
|
An zwei verschiedenen Stellen A und B in einer Stadt wurden Geschwindigkeitskontrollen
durchgeführt. Dabei wurden an der Stelle A dreimal so
viele Autos kontrolliert wie an der Stelle B. Die folgenden Tabellen geben
Auskunft über die dabei gemachten Beobachtungen (GÜ steht für
Geschwindigkeitsübertretung, männlich bzw. weiblich für das Geschlecht
des jeweiligen Fahrzeuglenkers):
a) Zeigen Sie, dass sowohl an der Stelle A als auch an der Stelle B der Anteil derjenigen, die die Geschwindigkeit übertreten haben, unter den Frauen größer ist als unter den Männern.
|
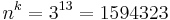
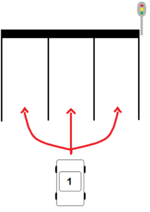
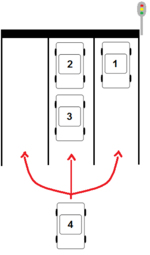
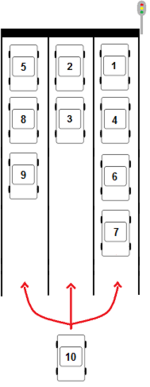
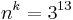 verschiedene Verteilungsmöglichkeiten.
verschiedene Verteilungsmöglichkeiten.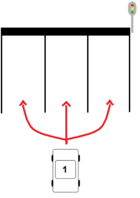
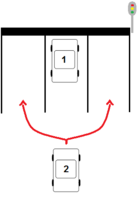
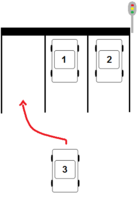
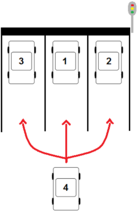
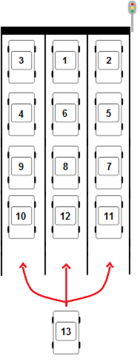
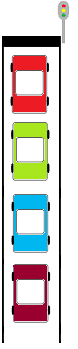
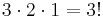 verschiedenen Arten an der Ampel anordnen. Diese drei Autos werden nachfolgend zu einer Gruppe zusammengefasst. Bei insgesamt 13 Autos gibt es 4 solcher Gruppen zuzüglich dem 13. Auto, dass wie im Bild verdeutlicht erneut 3 Wahlmöglichkeiten hat.
verschiedenen Arten an der Ampel anordnen. Diese drei Autos werden nachfolgend zu einer Gruppe zusammengefasst. Bei insgesamt 13 Autos gibt es 4 solcher Gruppen zuzüglich dem 13. Auto, dass wie im Bild verdeutlicht erneut 3 Wahlmöglichkeiten hat.
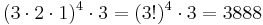
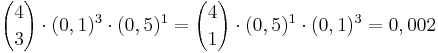
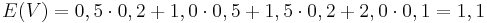
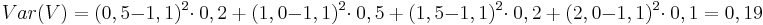
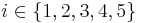 besitzen die gleiche mittlere Verzögerung
besitzen die gleiche mittlere Verzögerung 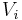 , die jeweils gleich dem Erwartungswert von V ist.
, die jeweils gleich dem Erwartungswert von V ist.