Quintenzirkel: Unterschied zwischen den Versionen
(→Exkurs: Division mit Rest:) |
(→Exkurs: Division mit Rest:) |
||
| Zeile 4: | Zeile 4: | ||
<div style="orange:0px; margin-right:90px; border: solid orange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> n = k <math>\cdot</math> m + r<br></div> | <div style="orange:0px; margin-right:90px; border: solid orange; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> n = k <math>\cdot</math> m + r<br></div> | ||
| − | gilt.“<br><br> | + | gilt.“<ref>Reimer S.28</ref><br><br> |
Beispiel:<br> | Beispiel:<br> | ||
| Zeile 25: | Zeile 25: | ||
„Allgemein wird also der Ton u, das heißt die Oktavfolge {u}, durch den (kleinsten nichtnegativen) Divisionsrest r bei Division durch 12 gekennzeichnet, also durch die für alle Töne der Folge mit einem r Element {0,1,...,11} gemeinsam geltende Kongruenz <br><br> | „Allgemein wird also der Ton u, das heißt die Oktavfolge {u}, durch den (kleinsten nichtnegativen) Divisionsrest r bei Division durch 12 gekennzeichnet, also durch die für alle Töne der Folge mit einem r Element {0,1,...,11} gemeinsam geltende Kongruenz <br><br> | ||
| − | Φ(u) ≡ r mod (12).“<br><br> | + | Φ(u) ≡ r mod (12).“<ref>ebenda S.29</ref><br><br> |
u entspricht dem in unserem Beispiel benannten t.<br> | u entspricht dem in unserem Beispiel benannten t.<br> | ||
| Zeile 50: | Zeile 50: | ||
Wir sehen, dass jeder Rest mod (12) nur einmal vorkommt und dabei die Werte 0,1,...,11 annimmt, | Wir sehen, dass jeder Rest mod (12) nur einmal vorkommt und dabei die Werte 0,1,...,11 annimmt, | ||
| − | wobei man für k = 12 wieder am Ausgangston angekommen ist. <br>Die Reihenfolge ergibt den uns bekannten Quintenzirkel<br><br> | + | wobei man für k = 12 wieder am Ausgangston angekommen ist.<ref>vgl. ebenda S.29 f.</ref> <br>Die Reihenfolge ergibt den uns bekannten Quintenzirkel<br><br> |
[[Bild:quintenzirkel1.jpg|450px|]]<br> | [[Bild:quintenzirkel1.jpg|450px|]]<br> | ||
<br><br> Hinter dem Quintenzirkel steht aus mathematischer Sicht der sogenannte [http://mspcdip.mathematik.uni-karlsruhe.de/Blaetter/proseminar/pdf/Chinesischer%20Restsatz.pdf Chinesischen Restsatz] ([http://de.wikibooks.org/wiki/Beweisarchiv:_Algebra:_Ringe:_Chinesischer_Restsatz Beweis des Satzes]).<br><br> | <br><br> Hinter dem Quintenzirkel steht aus mathematischer Sicht der sogenannte [http://mspcdip.mathematik.uni-karlsruhe.de/Blaetter/proseminar/pdf/Chinesischer%20Restsatz.pdf Chinesischen Restsatz] ([http://de.wikibooks.org/wiki/Beweisarchiv:_Algebra:_Ringe:_Chinesischer_Restsatz Beweis des Satzes]).<br><br> | ||
[[Benutzer:Grieninger_Sebastian/Facharbeit/temperierte Stimmung| ''weiter zur gleichstufig temperierten Stimmung'']] <br><br> | [[Benutzer:Grieninger_Sebastian/Facharbeit/temperierte Stimmung| ''weiter zur gleichstufig temperierten Stimmung'']] <br><br> | ||
[[Benutzer:Grieninger_Sebastian/Facharbeit|zurück zur Übersichtsseite]] | [[Benutzer:Grieninger_Sebastian/Facharbeit|zurück zur Übersichtsseite]] | ||
| + | ---- | ||
| + | <references /> | ||
Version vom 20. Dezember 2010, 05:59 Uhr
Exkurs: Division mit Rest:
„Ist eine Zahl 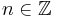 gegeben und ist
gegeben und ist  , m ≠ 1, eine weiter Zahl, der Divirsor, so kann man n durch m mit Rest dividieren. Das heißt, es gibt eine Zahl k Element Z und einen Rest r, r Element {0, 1, … , m – 1}, so daß
, m ≠ 1, eine weiter Zahl, der Divirsor, so kann man n durch m mit Rest dividieren. Das heißt, es gibt eine Zahl k Element Z und einen Rest r, r Element {0, 1, … , m – 1}, so daß
 m + r
m + rgilt.“[1]
Beispiel:
Für n = 25 und m = 7:
25 = 3  7 + 4; mit 4
7 + 4; mit 4 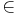 {0,1,2,3,4,5,6};
{0,1,2,3,4,5,6};
Dafür schreibt man: n ≡ r mod (m);
Für alle Töne t der Oktavfolge {…,c,c',...} gilt:
Φ(t) = k  12 + 0
12 + 0
Für alle Töne der Oktavfolge {…,cis,cis',...}:
Φ(t) = k  12 +1
12 +1
„Allgemein wird also der Ton u, das heißt die Oktavfolge {u}, durch den (kleinsten nichtnegativen) Divisionsrest r bei Division durch 12 gekennzeichnet, also durch die für alle Töne der Folge mit einem r Element {0,1,...,11} gemeinsam geltende Kongruenz
Φ(u) ≡ r mod (12).“[2]
u entspricht dem in unserem Beispiel benannten t.
Nun wollen wir die iterierten Quinten über dem Ton c betrachten.
Es sind die Töne t für die Φ(t) = k  7 für k = (0),1,2,... gilt.
7 für k = (0),1,2,... gilt.
Dies sind die Töne die die Kongruenz Φ(t) ≡ 0 mod (7) lösen.
Wenn wir nun k Element [0;12] einsetzen erhalten wir folgendes:
 7 ≡ 0 mod (12) bedeutet {c}
7 ≡ 0 mod (12) bedeutet {c} 1  7 ≡ 7 mod (12) bedeutet {g}
7 ≡ 7 mod (12) bedeutet {g}
2  7 ≡ 2 mod (12) bedeutet {d}
7 ≡ 2 mod (12) bedeutet {d}
3  7 ≡ 9 mod (12) bedeutet {a}
7 ≡ 9 mod (12) bedeutet {a}
4  7 ≡ 4 mod (12) bedeutet {e}
7 ≡ 4 mod (12) bedeutet {e}
5  7 ≡ 11 mod (12) bedeutet {h}
7 ≡ 11 mod (12) bedeutet {h}
6  7 ≡ 6 mod (12) bedeutet {fis}
7 ≡ 6 mod (12) bedeutet {fis}
7  7 ≡ 1 mod (12) bedeutet {cis}
7 ≡ 1 mod (12) bedeutet {cis}
8  7 ≡ 8 mod (12) bedeutet {gis}
7 ≡ 8 mod (12) bedeutet {gis}
9  7 ≡ 3 mod (12) bedeutet {dis}
7 ≡ 3 mod (12) bedeutet {dis}
10  7 ≡ 10 mod (12) bedeutet {ais}
7 ≡ 10 mod (12) bedeutet {ais}
11  7 ≡ 5 mod (12) bedeutet {f}
7 ≡ 5 mod (12) bedeutet {f}
 7 ≡ 0 mod (12) bedeutet {c}
7 ≡ 0 mod (12) bedeutet {c}Wir sehen, dass jeder Rest mod (12) nur einmal vorkommt und dabei die Werte 0,1,...,11 annimmt,
wobei man für k = 12 wieder am Ausgangston angekommen ist.[3]
Die Reihenfolge ergibt den uns bekannten Quintenzirkel
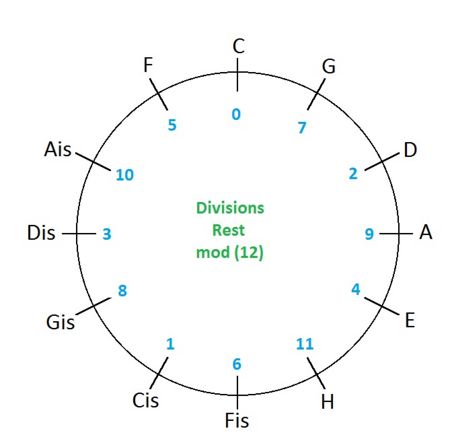
Hinter dem Quintenzirkel steht aus mathematischer Sicht der sogenannte Chinesischen Restsatz (Beweis des Satzes).
weiter zur gleichstufig temperierten Stimmung
zurück zur Übersichtsseite

