Q12 Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 9: | Zeile 9: | ||
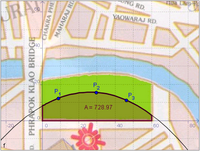
;Das Flächenproblem | ;Das Flächenproblem | ||
| − | {| | + | ::{| |
|[[Bild:Integral Grundstück.png|200px|left]] | |[[Bild:Integral Grundstück.png|200px|left]] | ||
|Ziel der folgenden Überlegungen ist es, ein Verfahren zu entwickeln, mit dem Flächeninhalte von krummlinig begrenzten Flächen berechnet werden können. | |Ziel der folgenden Überlegungen ist es, ein Verfahren zu entwickeln, mit dem Flächeninhalte von krummlinig begrenzten Flächen berechnet werden können. | ||
| Zeile 19: | Zeile 19: | ||
;Unter- und Obersumme | ;Unter- und Obersumme | ||
[[bild:Int_abb1.png|220px|right]] | [[bild:Int_abb1.png|220px|right]] | ||
| − | + | :Begriffsklärung [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/unterobersumme.htm Unter- und Obersumme] | |
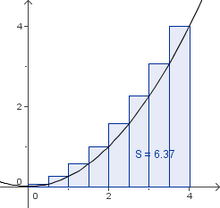
| − | + | :'''Aufgabe''': Gegeben ist die Funktion f(x) = 0.25 x². | |
| − | #Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. | + | ::#Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. |
| − | #Berechne die zugehörige Ober- und Untersumme. | + | ::#Berechne die zugehörige Ober- und Untersumme. |
| − | #Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an. | + | ::#Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an. |
| − | # Lösung: | + | ::# Lösung: |
<popup name="Lösung"> | <popup name="Lösung"> | ||
Wir zerlegen das [0;4] in 8 Teilintervalle. Jedes Teilintervall ist 0,5 breit. <br>Zu den x-Werten 0; 0,5; 1; 1,5;.....4 gehören die folgenden y-Werte: | Wir zerlegen das [0;4] in 8 Teilintervalle. Jedes Teilintervall ist 0,5 breit. <br>Zu den x-Werten 0; 0,5; 1; 1,5;.....4 gehören die folgenden y-Werte: | ||
| Zeile 40: | Zeile 40: | ||
</popup> | </popup> | ||
| − | + | :Berechnung von Unter- und Obersummen mit [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/unterobersumme_geogebra.htm GeoGebra] | |
;Integralfunktion | ;Integralfunktion | ||
| − | + | :[http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/integralfkt/integralfkt2.html Veranschaulichung durch GeoGebra-Applet] | |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 52: | Zeile 52: | ||
=== 2. Binomialverteilung=== | === 2. Binomialverteilung=== | ||
[[Bild:Binomial Distribution.PNG|300px|right]] | [[Bild:Binomial Distribution.PNG|300px|right]] | ||
| − | + | :[[Media:Binomialverteilung Aufgabentypen.doc|Aufgabentypen mit Lösung]] | |
| + | :[[Media:Lösungen LS12 Seite 86 Nr 7-24.doc|Lösungen LS Seite 86 Nr 7-24]] | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 11. Dezember 2010, 19:59 Uhr
1. Integralrechnung
|
2. Binomialverteilung |
3. Hausaufgaben |
- Kapitel aus dem Buch: Kapitel 2
 0,5 + f (1)
0,5 + f (1) 
