Facharbeit Lernpfad Terme/Addieren und Subtrahieren von Termen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
K
K
Zeile 86: Zeile 86:
  
  
 +
 +
<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>'''
 
Prüfe, ob die Terme äquivalent sind
 
Prüfe, ob die Terme äquivalent sind
 
<div class="multiplechoice-quiz">
 
<div class="multiplechoice-quiz">
Zeile 128: Zeile 130:
 
</div>
 
</div>
  
−
}}
+
<br><br><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br />
  
−
<br><br>
+
</div>

Version vom 12. August 2010, 13:56 Uhr

Addieren und Subtrahieren von Termen

Äquivalente Terme




Übertrage die Zeichnung in dein Heft und überlege dir zwei verschiedene Terme, mit denen du den Flächeninhalt der grün markierten Fläche ausrechnen kannst. (Hinweis: b1=b2=b)


Tipp: In der vorherigen Aufgabe gab es auch 2 Möglichkeiten den Flächeninhalt zu errechnen.



Einstieg addierensubtrahieren neu.jpg


Erklärung:

Zwei Terme, die bei jeder möglichen Einsetzung einer Zahl für die Variable jeweils den gleichen Wert annehmen heißen gleichwertig oder äquivalent. Durch Anwendung der Rechengesetze kannst du einen Term in einen äquivalenten Term umformen.

Rechengesetze:

  • Kommutativgesetz (KG): für alle rationalen Zahlen a, b gilt:
a+b = b+a
a•b = b•a
  • Assoziativgesetz (AG): für alle rationalen Zahlen a, b, c gilt:
a+(b+c) = (a+b)+c = a+b+c
a•(b•c) = (a•b)•c = a•b•c
  • Distributivgesetz (DG): für alle rationalen Zahlen a, b, c gilt:
a•(b+c) = a•b+a•c
für alle rationalen Zahlen a, b, c (c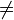\neq 0) gilt:
(b+c):a = b:a+c:a


Beispiel:

T(a;b)= 3a+(7b+2a)

(KG)= 3a+(2a+7b)
(AG)= (3a+2a)+7b
= 5a+7b

Durch geschicktes Anwenden der Rechengesetze kannst du einen Term zu einem äquivalenten Term vereinfachen. Vereinfache nun selbst folgende Terme:

a)T(a;b)= 7a+(9b+6a)

b)T(a;b)= 2•(a•3)•b+4•(a•5)•b

c)T(a;b)= (3+5•x)•x


Aufgabe 1:

Prüfe, ob die Terme äquivalent sind

1:

T1 (x)= 5x-2x+6x

T2 (x)= 2•x•2+5x (äquivalent) (!nicht äquivalent)

2 :

T1 (y)= 4y-3•4y+15

T2 (y)= 3•5+2y-4y-6y

(!äquivalent) (nicht äquivalent)

3:

T1 (y;z)= 2y-3+z

T2 (y;z)= 5y•2+z+5-8y-8

(äquivalent) (!nicht äquivalent)

4:

T1 (z)= 4•\frac{3}{2} -2z

T2 (z)= 6+8z-5•20%-z•9

(!äquivalent) (nicht äquivalent)

5:

T1 (r)= 3r-23 r+5-r

T2 (r)= 3•r•2 (!äquivalent) (nicht äquivalent)









































Von „http://rmg.zum.de/index.php?title=Facharbeit_Lernpfad_Terme/Addieren_und_Subtrahieren_von_Termen&oldid=34332“