Facharbeit Lernpfad Terme/Aufstellen und Interpretieren von Termen: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (→Aufstellen von Termen) |
K |
||
| Zeile 178: | Zeile 178: | ||
| | | | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild:drachenviereck. | + | [[Bild:drachenviereck.png]] <br /> <br /> |
|} | |} | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | Das Drachenviereck besteht aus 2 großen (wegen der Achsensymmetrie: gleichgroßen) Dreiecken. Deshalb | + | Das Drachenviereck besteht aus 2 großen (wegen der Achsensymmetrie: gleichgroßen) Dreiecken. Deshalb rechnet man den Flächeninhalt eines Teildreiecks aus und verdoppelt ihn dann. Der Flächeninhalt eines Dreiecks ist allgemein: A<sub>D</sub> <math>\frac{1}{2}</math> <span style="color: darkblue">a</span>•<span style="color: darkorange">h<sub>a</sub> |
</span> | </span> | ||
| − | In diesem Fall also: A<sub>D</sub> = <math>\frac{1}{2}</math> <span style="color: darkblue">( | + | In diesem Fall also: A<sub>D</sub> = <math>\frac{1}{2}</math> <span style="color: darkblue">(m+n)</span>•<span style="color: darkorange">2</span> = (m+n)•2•<math>\frac{1}{2}</math> = (m+n)•1 |
| − | Um den Flächeninhalt des Drachenvierecks A<sub>DV</sub> zu erhalten, muss man den Flächeninhalt des Teildreiecks verdoppeln: '''A<sub>DV</sub>''' = 2•A<sub>D</sub> = 2•( | + | Um den Flächeninhalt des Drachenvierecks A<sub>DV</sub> zu erhalten, muss man den Flächeninhalt des Teildreiecks verdoppeln: '''A<sub>DV</sub>''' = 2•A<sub>D</sub> = 2•(m+n)= '''2•(m+n)''' |
| − | <u>Hinweis:</u> Es gibt eine weitere Lösung | + | <u>Hinweis:</u> Es gibt eine weitere Lösung, wenn man das Drachenviereck in 2 andere Dreiecke aufteilt. |
| − | Der Flächeninhalt kann auch so bestimmt werden: A<sub>DV</sub>= ( | + | Der Flächeninhalt kann auch so bestimmt werden: A<sub>DV</sub>= (4•<math>\frac{n}{2}</math> )+(4•<math>\frac{m}{2}</math> ) |
Das Ergbenis ist gleich. | Das Ergbenis ist gleich. | ||
| − | * A(8cm;2cm)= | + | * A(8cm;2cm)= 2cm(8cm+2cm)=2cm•10cm= 20cm<sup>2</sup> |
| − | * A(10cm;5cm)= | + | * A(10cm;5cm)= 2cm(10cm+5cm)= 2cm•15cm= 30cm<sup>2</sup> |
| − | * A(12cm;9cm)= | + | * A(12cm;9cm)= 2cm(12cm+9cm)= 2cm•21cm= 42cm<sup>2</sup> |
| − | * A(15cm;13cm)= | + | * A(15cm;13cm)= 2cm(15cm+13cm)= 2cm•28cm= 56cm<sup>2</sup> |
</popup> </div> | </popup> </div> | ||
Version vom 12. August 2010, 08:53 Uhr
Aufstellen und Interpretieren von Termen
Aufstellen von Termen
|
|
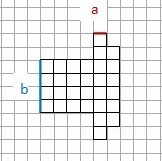
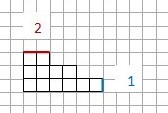
Setze nun für a=1cm und b=4cm ein
Erklärung:
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Rezept
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
Beispiel:
|
|
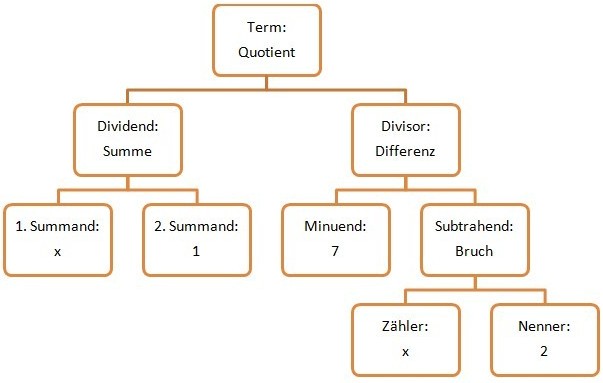
Aufgabe 2:Gib den Term zu folgendem Gliederungsbaum an und berechne seinen Wert für x=4!
Aufgabe 3:Laura hat zu schnell von der Tafel abgeschrieben. Dabei hat sie die Werte der Variablen vergessen, nur die Ergebnisse hat sie noch. Hilf ihr die passenden Werte für die Variablen zu finden, wenn der Term T(n)=n2+2 lautete.
Warum gibt es meist zwei Möglichkeiten?
a) T(?)= 18
b) T(?)= 38
c) T(?)= 3
d) T(?)= 6
Aufgabe 4:
|
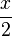 )
)
 ) = 5:(7-2) = 5:5 = 1
) = 5:(7-2) = 5:5 = 1

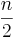 )+(4•
)+(4•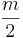 )
)

